Задача №4.

Задана кодовая комбинация простого первичного кода Q(0,1)

Требуется:

1) закодировать ее помехоустойчивым циклическим кодом, исправляющим однократную ошибку (t_испр.=1);

2) проверить правильность построения кодовой комбинации циклического кода F(0,1);

3) составить таблицу синдромов циклического кода;

4) проверить, будет ли исправлена однократная ошибка в i – м разряде кодовой комбинации циклического кода;

5) построить структурную схему кодера циклического кода.

Исходные данные:

Последняя цифра зачетной книжки 3 = 11

Предпоследняя цифра зачетной книжки 7 = 01

K=1101

i = 4

Кодовая комбинация: 1101 (к=4)

1) Минимальное кодовое расстояние определяется по формуле:

, (6) где - кратность исправляемых ошибок;

Определим количество проверочных элементов при к=4, по формуле:

(7)

Общая длина кодовой комбинации:

, где к – длина кодовой комбинации простого кода (к=4);

Исходная кодовая комбинация циклического кода будет иметь вид (7,4).

2) Образующий полином

G(x)=x³+x+1 или в двоичной записи (1001)

R(x)=Q(x)·x^r/G(x), где Q(x)·x^r = (x³+ x²+ x)· x³ = x⁶+ x⁵+ x⁴ = 1101000

Найдем остаток от деления Q(x) на G(x)

R(x) =1101000 1001

1001 11

0100000

1001

100 – R(x)

R(x) =100

F (x) = Q(x) ·x^r + R(x)

F (0,1) = 1110000

+ 100

1110100

Проверка:

1100100 1001

1001 11

0100100

1001

000000 – R(x)=0

3) Составляем таблицы синдромов.

– образующая матрица.

Q1(x) = 1000 Q1(x) ·x³ / G(x) = 001

Q2(x) = 0100 Q2(x) ·x³ / G(x) = 010

Q3(x) = 0010 Q3(x) ·x³ / G(x) = 100

Q4(x) = 0001 Q4(x) ·x³ / G(x) = 001

G7,4=	0	0	0	1	0	0	1
	0	0	1	0	0	1	0
	0	1	0	0	1	0
	1	0	0	0	0	0	1

Проверочная матрица:

H7,3=	0	0	1	0	0	0	1
	0	1	0	0	0	1	0
	1	0	0	1	1	0	0

Транспонирую строки матрицы в столбцы получим матрицу синдромов:

С3,7=	0	0	1	7
	0	1	0	6
	1	0	0	5
	0	0	1	4
	0	0	1	3
	0	1	0	2
	1	0	0	1

4) С помощью матрицы синдромов можно обнаружить ошибку в любом разряде.

Ошибка в i =4 разряде

Исходная комбинация 1¹1²0³1⁴1⁵0⁶0⁷

Принятая комбинация 1¹1²0³0⁴1⁵0⁶0⁷

1100100 1001

1001 111

01011

01001

001000

1011

001= R(x) ошибка в 4 разряде, поэтому инвертируем неправильный 0 на 1, получим правильную кодовую комбинацию.

5) Построим структурную схему кодера циклического кода.

Упрощенная структурная схема кодера приведена на рисунке 1. Такая схема содержит регистр задерж­ки RG, обеспечивающий сдвиг информационной группы на четы­ре такта, и формирователь проверочной группы, включающий ре­гистры сдвига и сумматоры по модулю 2 в цепи обратной связи. В схеме также имеются два ключа K1 и K2, обеспечивающие не­обходимую последовательность функционирования. В положении, когда K1 замкнут, а K2 разомкнут, информационная часть кода подается на вход схемы, т. е. в первую ячейку регистра задерж­ки, и через S1 в первую ячейку сдвига. По окончании четырех тактов старший разряд инфор­мационной группы записывает­ся в последние ячейки обоих регистров. Во время пятого такта информационная группа начинает поступать на выход схемы. С этого момента K1 раз­мыкается, а К2 замыкается. Начиная с пятого такта фор­мирователь проверочной груп­пы будет функционировать в соответствии с ранее описанной про­цедурой. После девятого такта размыкается, а K1 замыкается. С этого момента формирователь проверочной группы работает как обычный регистр сдвига, выталкивая на выход записанные в ячей­ках кодовые импульсы проверочной группы. Одновременно в регистры начинает поступать новая группа информационных элементов.

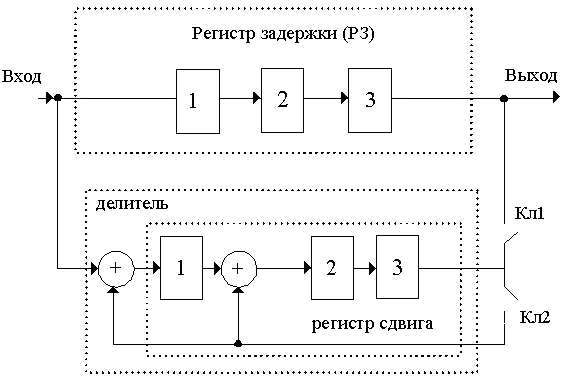
Рисунок 11. Кодер циклического кода.