19. Относительные показатели

Относительный показатель – результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических явлений.

Без относительных показателей невозможно измерить интенсивность развития изучаемого явления во времени, оценить уровень развития одного явления на фоне других, взаимосвязанных с ним явлений, осуществить пространственно-территориальные сравнения. При расчете относительного показателя абсолютный показатель, находящийся в числителе получаемого отношения, называется текущим или сравниваемым, а показатель, находящийся в знаменателе, называется базой сравнения или основой.

Относительные показатели могут выражаться в коэффициентах, процентах, промилле, продецимилле, а могут быть именованными значениями. Проценты используются в тех случаях, когда сравниваемый абсолютный показатель превосходит базисный не более, чем в 2-3 раза. Если же превосходство больше, то используется коэффициент.

20. Средняя величина представляет собой обобщенную количественную характеристику признака статистической совокупности в конкретных условиях места и времени.

Показатель в форме средней величины отражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков.

Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием основных.

Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности.

Исходное соотношение средней

На практике определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:

Данная формула является основополагающей. В зависимости от того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение.

Различают следующие виды средней, каждая из которых может быть простой и взвешенной:

• Средняя арифметическая;

• Средняя гармоническая;

• Средняя геометрическая;

• Средняя квадратическая, кубическая и т.д.

• Структурные средние: мода и медиана.

21 Средняя арифметическая и её свойства

Средняя арифметическая простая (не взвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по не сгруппированным данным.

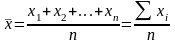
Средняя арифметическая взвешенная. При расчете средних величин отдельные значения признака могут повторяться, встречаться по нескольку раз. В данном случае расчет проводится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.

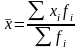
Свойства средней арифметической

Средняя арифметическая величина имеет следующие свойства, использование которых упрощает ее расчет.

1) Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты.

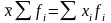
2) Сумма отклонений индивидуального значения признака от средней арифметической равна нулю:

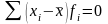
3) Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на туже величину.

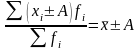
4) Если все варианты значений признака уменьшить или увеличить в А раз, то средняя соответственно уменьшится или увеличится в А раз:

5) Если все частоты уменьшить или увеличить в А раз, то средняя останется неизменной:

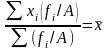
6) Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:

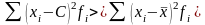
22. Понятие и классификация рядов динамики

Ряд динамики – последовательность изменяющихся во времени значений статистического показателя, распложенного в хронологическом порядке.

Составными элементами ряда динамики являются показатели уровней ряда (статистический показатель, характеризующий данное явление за период или на момент времени) и периоды времени (годы, кварталы, сутки) или моменты (даты) времени (периоды времени, которым относятся статистические данные об изучаемом явлении).

Уровни ряда обычно обозначаются через «у», моменты или периоды времени, к которым относятся уровни – через «t».

1. В зависимости от способа выражения уровней ряда ряды динамики делятся на ряды: а) абсолютных; б) относительных; в) средних величин.

2. В зависимости от того, как выражают уровни ряда (на начало месяца или за период), выделяют моментные и интервальные ряды динамики.

3. В зависимости от расстояния между уровнями ряды динамики бывают с равноотстоящими и неравноотстоящими уровнями во времени.

4. В зависимости от наличия основной тенденции изучаемого процесса ряды динамики подразделяются на стационарные и нестационарные.

23 Сопоставимость уровней ряда динамики.

При построении динамических рядов следует помнить, что уровни его должны быть сопоставимы между собой, т.к. для несопоставимых величин невозможно вести расчеты показателей динамики. Уровни ряда динамики могут быть несопоставимы по следующим причинам: несопоставимость по территории (изменения границ). В этом случае старые (прежние) данные пересчитывают в новые границы, о чем делается оговорка; несопоставимость вследствие различных единиц измерения и единиц счета. Нельзя, например, сравнивать производство тканей в погонных метрах и в квадратных метрах. Несопоставимость по методологии учета или расчета показателей. Обычно для достижения сопоставимости прежние показатели пересчитывают по новой методологии, о чем делается оговорка. ^ Несопоставимость по кругу охватываемых объектов, которая возникает вследствие ряда организационных причин, например, перехода объектов из одного подчинения в другое. В этом случае сопоставимость достигается смыканием рядов динамики

Смыканием рядов динамики называют объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или в разных территориальных единицах, или охватывающих различное количество объектов. Сопоставимы ряд можно при этом можно получить в абсолютных величинах и можно в относительных.

24. Показатели изменения уровней ряда

Существует две категории показателей

1) Средние уровни ряда определяются для интервальных рядов с равноотстоящими интервалами по формуле средней арифметической простой

; n – число уровней ряда

Для интервального ряда с неравноотстоящими интервалами средние уровни ряда определяется по формуле средней арифметической взвешенной

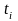; - длительность интервала времени между уровнями

Для моментных рядов с равноотстоящими интервалами средние уровни ряда определяются по формуле средней хронологической простой

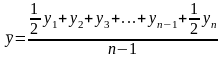; n – количество дат

Для моментных рядов с неравноотстоящими датами средние уровни ряда определяются по формуле средней хронологической взвешенной

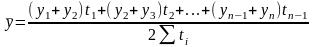
- период времени между двумя смежными датами

2) Средние показатели изменения уровней ряда определяется по цепным показателям

Средний абсолютный прирост (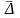 ) – обобщющий показатель скорости изменения явления во времени

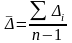; n – количество дат или периодов времени

Данный показатель позволяет установить, на сколько в среднем за единицу времени должен увеличиваться уровень ряда, чтобы отправляясь от начального уровня, за данное число периодов достигнуть конечного уровня.

Средний коэффициент роста (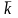 ) и средний темп роста ( )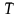

Средний коэффициент роста определяется по формуле средней геометрической простой

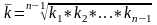
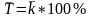
Средний темп роста показывает, сколько процентов в среднем должен составлять рост показателя в течение определенного периода времени, чтобы достигнуть конечного значения.

Средний темп прироста показывает на сколько в среднем ежегодно возрастат изучаемый показатель.

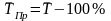
25. Основные приёмы выравнивания ряда динамики

Очень часто в рядах динамики сложно определить общую тенденцию развития. Второй задачей рядов динамики является выявление таких периодов развития, которые достаточно однородны по своим условиям и взаимодействиям связей между показателями.

Под тенденцией понимается общее направление к росту, снижению или стабилизации уровня явления с течением времени. Тенденция по периодам может не совпадать с общей тенденцией. Иногда вообще сложно определить общую тенденцию. В этом случае прибегают к различным методам:

1. способ укрупнения интервалов;

2. сглаживание ряда с помощью скользящей средней;

3. производят аналитическое выравнивание и получают уравнение тренда.

Первый способ заключается в переходе от меньших временных интервалов к большим и расчете усредненных уровней ряда за укрепленный интервал. Поэтому для наглядного представления тренда применяется метод укрупнения интервалов.

Способ скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней ряда, начиная со второго, далее – начиная с третьего и т.д

Метод скользящей средней волне приемлем, если графическое изображение ряда динамики напоминает прямую линию. Однако когда тренд выравниваемого ряда имеет изгибы, использовать для сглаживания ряда метод скользящей средней нецелесообразно.

Но самые точные результаты выравнивания ряда динамики дает аналитическое выравнивание, с помощью которого строят математическое уравнение, наилучшим образом описывающее тенденцию изменения показателя ряда.

При построении тренда необходимо выявить этапы в развитии исследуемого явления с помощью абсолютных и относительных показателей рядов динамики, выбрать тип линии уравнения тренда и вычислить параметры уравнения. Для этого, как правило, применяют метод наименьших квадратов