Практическая № 11

Уклон и конусность

Уклоны. ГОСТ 8908-81.

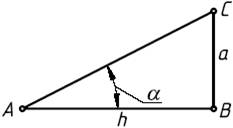
Уклон – это величина, характеризующая наклон одной линии (плоскости) по отношению к другой, i = tg a = ВС/АВ.

Д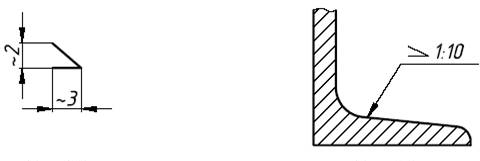 ля обозначения уклонов на чертеже применяется знак (рис1) по ГОСТ 2.304-81 (размеры знака даны для шрифта № 5). Знак наносится перед размерным числом, острый угол знака должен быть направлен в сторону уклона (рис 2)

П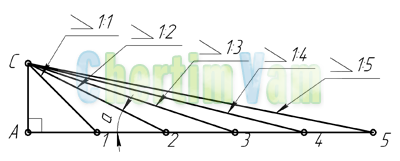 остроение уклона. На примере (рисунок) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

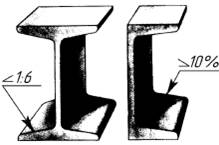
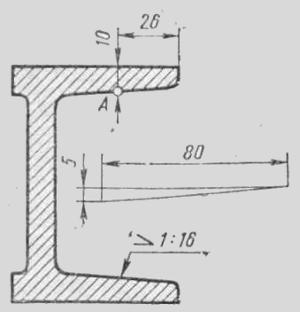
На рисунке в качестве примера построен профиль несимметричного двутавра, правая полка которого имеет уклон 1:16. Для ее построения находят точку А с помощью заданных размеров 26 и 10. В стороне строят линию с уклоном 1:16, для чего по вертикали откладывают, например, 5 мм, а по горизонтали 80 мм; проводят гипотенузу, направление которой определяет искомый уклон. С помощью рейсшины и угольника через точку А проводят линию уклона, параллельную гипотенузе.

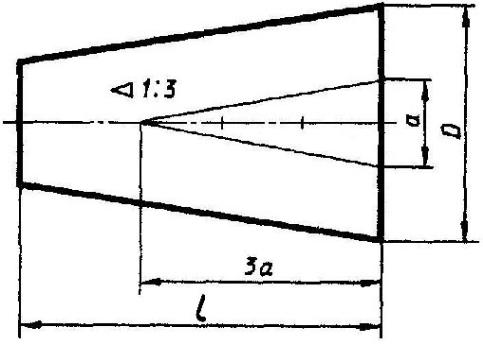
Конусности. ГОСТ 8593-81

Конусность – это отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними (рис. 1.4)

C = (D – d) / L = 2 tg a / 2.

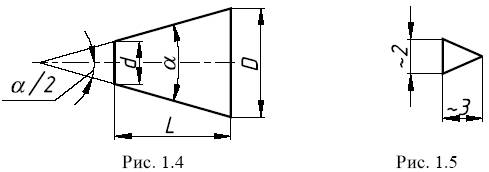
Для обозначения конусности на чертеже применяется знак (рис. 1.5) по ГОСТ 2.304-81 (размеры знака даны для шрифта № 5). Знак наносится перед размерным числом, характеризующим конусность, острый угол знака должен быть направлен в сторону вершины конуса (рис. 1.6).

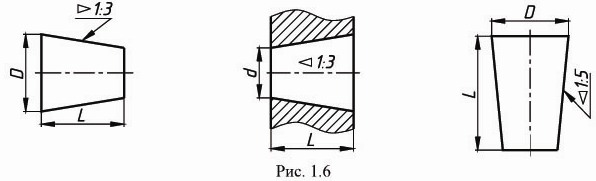
Если нужно построить конусность 1:n относительно заданной оси, то строим  уклоны 1:2n с каждой стороны оси.

 K = 2i.

Также построение конусности при заданной длине L и диаметре D одного из оснований можно выполнить графически следующим образом: построить на заданной оси вспомогательный полный конус, у которого произвольно взятое основание а укладывается в высоте столько раз, сколько задано в обозначении конуса. Затем провести образующие искомого конуса параллельно образующим вспомогательного конуса через концы заданного диаметра D, как показано на рисунке.

Самостоятельная работа № 2

Презентация по теме: Лекальные и коробовые кривые.

1) Рассмотреть построение лекальных кривых: параболы, гиперболы, синусоиды.

(http://youdraft.ru/ychebniemateriali/46-osnovniesvedeniia/106-lekalniekrivie.html )

2) Рассмотреть построение коробовых кривых: овала по заданным осям ав и cd и овоидальной кривой.

(http://youdraft.ru/ychebniemateriali/46-osnovniesvedeniia/101-cirkylniekrivie.html)

3) Создать презентацию «Лекальные и коробовые кривые»

Практическая работа № 12

Основы начертательной геометрии

Начертательная геометрия является одним из разделов геометрии, в котором пространственные фигуры, представляющие собой совокупность точек, линий, поверхностей, изучаются по их проекционным изображениям на плоскости (или какой-либо другой поверхности).

С древних времён человек пытался сохранить образ увиденного. Как сейчас сказали бы «в твердой копии». Так появилась наскальная живопись. Затем человек стал украшать рисунками стены своего жилища, посуду, орудия труда и другие предметы быта.

Постепенно, с развитием и разделением труда в проектной и производственной сферах деятельности, перед человечеством стали возникать все более серьезные технические задачи. Это создание проектной документации на строительство военных сооружений и жилых домов, мостов и дорог, орудий и предметов труда, составление схем и карт местности и т.п.

Различные сферы человеческой деятельности, развитие производства требовали выработки неких общих правил и стандартов технической документации.

Ещё греческие и римские учёные, начав с изучения науки о Земле, пытались выработать некоторые правила представления имеющейся пространственной геометрической информации на плоскости.

В эпоху Возрождения начинается расцвет архитектуры, скульптуры, живописи, что приводит к разработке теоретических основ перспективы. Основателем теоретической перспективы был итальянский учёный Л. Альберти (1404-1472). Гениальный итальянский учёный и художник Леонардо да Винчи (1452-1519) дополнил линейную перспективу учением «Об уменьшении цветов и отчётливости очертаний». Французский математик и архитектор Ж. Дезарг (1593-1662) впервые применил для построения перспективы метод координат, положив этим начало аксонометрическому методу в начертательной геометрии.

В 1795 году вышел труд «Начертательная геометрия» Гаспара Монжа (1746-1818), где он описал и обобщил накопленный годами опыт геометрических построений, систематизировал метод проекций, ввел понятие «комплексный чертёж». Развитию начертательной геометрии в нашей стране способствовали такие художники, зодчие и учёные как А. Рублёв, В. Баженов, А. Воронихин, И. Ползунов, И. Кулибин и другие. Первым русским профессором начертательной геометрии был Я. А. Севостьянов (1796-1849), который создал оригинальный курс начертательной геометрии. Далее начертательная геометрия в России развивалась, усилиями таких ученых, как Н. И. Макаров, В. И. Курдюмов, А. К. Власов, Н. А. Глаголев, Н. Ф. Четверухин и многие другие.

Велика роль начертательной геометрии в науке и производстве. Графическое изображение — единственное средство для получения, передачи и запоминания информации, поскольку более 90 % информации человек получает с помощью зрения. В техническом чертеже передается информация, необходимая для производства, поэтому чертеж является одним из основных производственных документов.

Начертательная геометрия — наука, изучающая методы построения изображений пространственных фигур на плоскости и способы решения пространственных задач при помощи полученных плоскостных изображений.

Начертательная геометрия является базовой дисциплиной для изучения таких инженерно-технических дисциплин как техническое рисование, черчение, архитектурная графика, детали машин и механизмов, теоретическая и строительная механика и др. Начертательная геометрия имеет особое значение для развития пространственного воображения, которое необходимо в практической деятельности, как инженера, так и дизайнера.

Прямой задачей начертательной геометрии является задача построения чертежа, т.е. однозначного отображения трехмерных предметов на плоскости и создание способов этого построения (прямое преобразование 3D → 2D). Обратной задачей является чтение чертежа, т.е. восстановление по проекционному чертежу формы и размеров оригинала, взаимного расположения его элементов и других геометрических параметров (обратное преобразование 2D → 3D).

Изображаемый предмет называют оригиналом или объектом исходного производства. Чертеж должен содержать геометрическую информацию о форме и размерах оригинала. К такому чертежу предъявляются следующие основные требования:

• Наглядность, т.е. давать пространственное представление об оригинале;

• Простота с точки зрения графического выполнения;

• Точность — графические операции, выполняемые на чертеже, должны давать достаточно точные решения.