Практическая работа № 9

Вычерчивание плоского контура детали с выполнением сопряжений (графическая работа)

Задание:

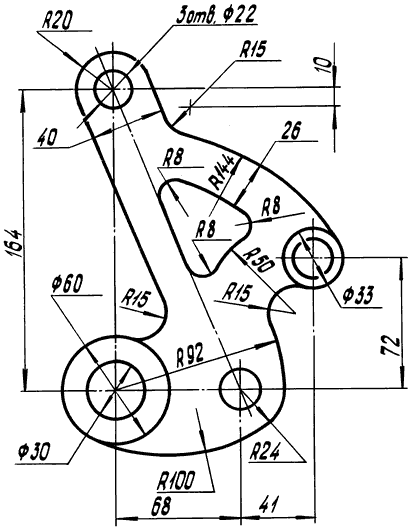
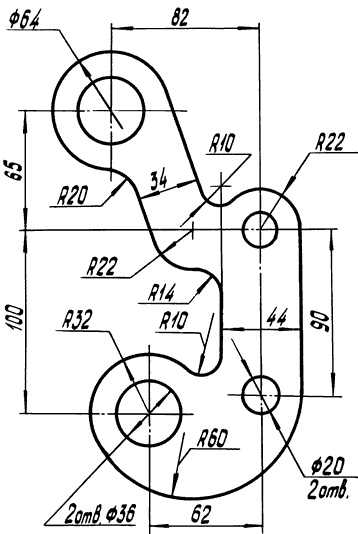
Построить изображение плоского контура детали с выполнением сопряжений на формате А4 (формат располагается вертикально). Масштаб-1:2. Исходные данные приведены ниже. Линии построения не стирать.

Цель работы: Изучение типов линий и приобретение навыков их выполнения (ГОСТ 2.303-68). Изучение построений сопряжений в очертаниях технических форм. Ознакомление с основными правилами нанесения размеров (ГОСТ 2.307-68). Изучение приемов написания букв и цифр чертежным шрифтом (ГОСТ 2.304-81). Применение масштаба.

Методика оформления и последовательность выполнения задания "Очертания технических форм":

1. Подготовить формат А4. Нанести внутреннюю рамку и прямоугольник основной надписи.

2. По размерам, нанесенным на исходные данные, установить габариты изображения и спланировать габаритный прямоугольник на чертеже так, чтобы очерк детали расположился примерно в середине поля формата.

3. Выбрать базовые линии очерка детали и нанести их на чертеже. Вычертить в тонких линиях контур детали, проведя все вспомогательные построения для центров и точек сопряжения линий.

4. Нанести выносные и размерные линии (ГОСТ 2.307-68). Особое внимание следует обратить на расположение размерных чисел над размерными линиями.

5. Сделать обводку чертежа.

6. Заполнить основную надпись чертежным шрифтом.

Вар. №	Контур детали	Вар. №	Контур детали
1		2

Практическая работа № 9

Лекальные кривые

Все множество плоских кривых можно разделить на циркульные и лекальные. Циркульной называют кривую, которую можно построить с помощью циркуля. К ним относятся окружность, овал и т.д.

Лекальной называют кривую, которую нельзя построить с помощью циркуля. Ее строят по точкам с помощью специального инструмента, называемого лекалом. К лекальным кривым относятся эллипс, парабола, гипербола, спираль Архимеда и др.

Лекальные кривые можно разделить на закономерные и незакономерные.

Закономерными называют кривые, которые можно задать алгебраическим выражением. Незакономерные кривые нельзя задать алгебраическим выражением.

Среди закономерных кривых наибольший интерес для инженерной графики представляют кривые второго порядка: эллипс, парабола и гипербола, с помощью которых образуются поверхности, ограничивающие технические детали.

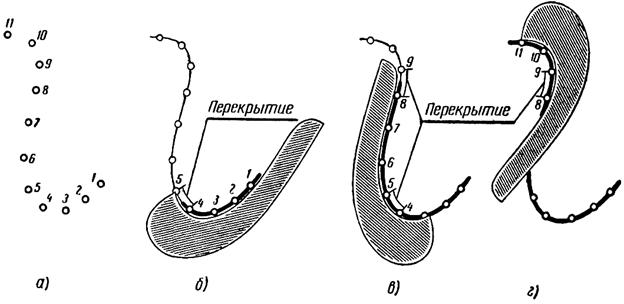
Лекальная кривая - это плавная кривая линия. Лекальную кривую нельзя даже частично провести с помощью циркуля. Лекальные кривые чертят с помощью лекал.

Рассмотрим построение лекальных кривых на примере Эллипса и Спирали Архимеда.

Эллипс — это замкнутая кривая. Его большая и малая оси есть оси симметрии эллипса. Точки F1 и F2 — это фокусы эллипса. Сумма расстояний от любой точки эллипса (от М, от N, ...) до фокусов F1 и F2 есть величина постоянная. Она равна большой оси АВ. Например, F1M + F2M. = AB; F1N + F2>N=AB (рис. 17). Пример построения эллипса приведен на рис.2.

.

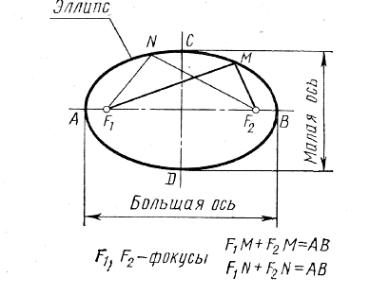
Рис. 1. Лекальная кривая – эллипс

Задача 1:

Построение лекальной кривой – эллипса

1.Даны большая ось АВ и малая ось CD эллипса

2. Проводим из центра О окружность радиуса ОА и окружность радиуса ОС.

3. Делим большую окружность на 12 равных частей. Точки деления 1, 2, 3 ... 12 окружности соединяем с центром О. Прямые 1—7, 2—8 ... 6—12 делят малую окружность тоже на 12 равных частей.4. Из точек деления большой окружности проводим прямые параллельные CD. Из точек деления малой окружности проводим прямые, пapaллельные АВ. Точки пересечения вертикальных и горизонтальных прямых — это искомые точки эллипса. 5. Соединяем точки плавной кривой с помощью лекал. (рис.2.).

Примечание: Радиусы окружностей для данной задачи: ОА=20, СD=60.

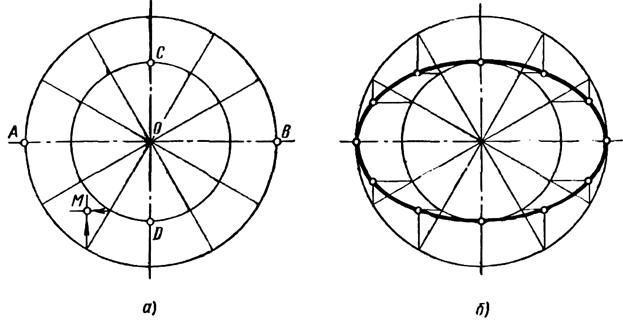
Рис. 2. Построение лекальной кривой – эллипса

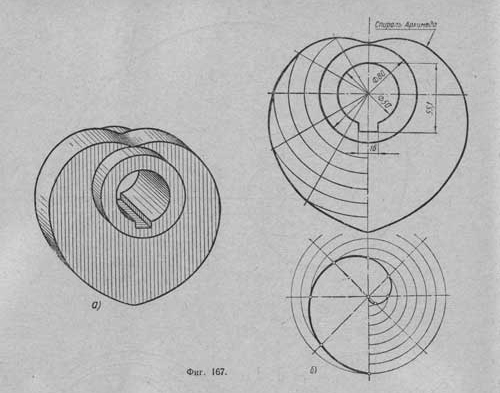
Спиралью Архимеда называется плоская кривая, полученная как след точки, движущейся равномерно поступательно от неподвижной точки О по выходящему из нее и равномерно вращающемуся вокруг точки О лучу (радиусу)Точка О называется полюсом спирали; отрезок ОА называется шагом t спирали; отрезок KL - нормалью спирали, а прямая MN, перпендикулярная к нормали, называется касательной; точка К может находиться в любом месте спирали, а точку L находят путем построения, для чего точку К соединяют прямой с точкой О и в точке О проводят перпендикуляр к отрезку КО, который пересечет в точке L окружность, проведенную из центра О диаметром D = t/3,14.

Задача 2:

Построение Архимедовой спирали

Заданный шаг t спирали Архимеда делят на несколько, например на восемь, равных частей. Из конца О отрезка / проводят окружность R = t и делят ее на столько же равных частей, на сколько был разделен шаг t. На первом луче путем проведения дуги радиусом O1 из центра О получают точку I, на втором луче путем проведения дуги радиусом O2 получают точку II и т.д. После того как на всех лучах будут получены точки I, II, III, IV, V, VI, VII и VIII, проводят через них кривую - спираль Архимеда.

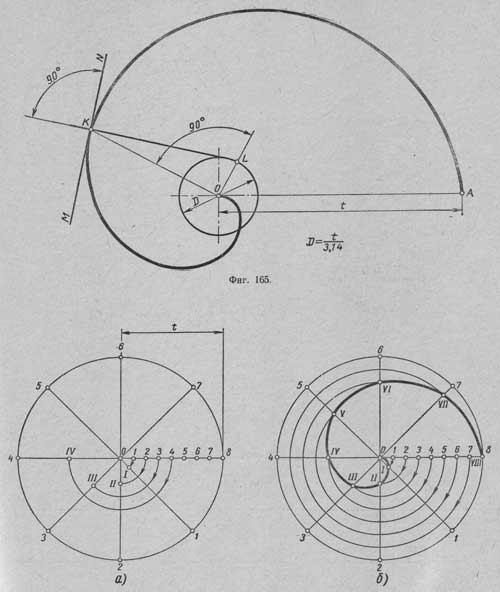
Примечание: для данной окружности R=t=55 На рисунке дано изображение распределительного кулачка. Очертания боковых сторон его выполняют по спирали Архимеда