
- •Теоретико методологические основы бизнес исследований в менеджменте
- •Согласование результатов исследовательского проекта и процесса принятия эффективных управленческих решений
- •Объект и предмет исследования в менеджменте
- •Принятие решения и менеджмент
- •Уровни принятия управленческих решений
- •Классификация проблем принятия решений
- •Физические модели и физическое моделирование
- •Математические модели и математическое моделирование
- •Статические математические модели
- •Детерминированнные математические модели
- •Стохастические математические модели и математические модели операций в условиях полной неопределенности
- •Оптимизационные математические модели
- •Основные понятия и определения в сетевых и потоковых моделях
- •Определение кратчайшего маршрута в сети
- •Транспортная задача условие баланса транспортной задачи
- •Транспортная задача с максимизацией целевой функции
Рациональные решения
В управлении принятие решений – более систематизированный процесс, чем в частной жизни. Это связано с много большей ответственностью.
Исследование операций
Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению какой-то цели. ^ Цель исследования операций - предварительное количественное обоснование оптимальных решений.Решение- Всякий определенный выбор зависящих от наспараметровОптимальным называется решение, по тем или другим признакам предпочтительнее перед другими. ^ Элементы решения- параметры, совокупность которых образует решение.Множествомдопустимых решений называются заданные условия, которые фиксированы и не могут быть нарушены. ^ Показатель эффективности - количественная мера, позволяющая сравнивать по эффективности разные решения. Все решения принимаются всегда на основе информации, которой располагает лицо принимающее решение (ЛПР). Каждая задача в своей постановке должна отражать структуру и динамику знаний ЛПР о множестве допустимых решений и о показателе эффективности. ^ Задача называется статической, если принятие решения происходит в наперед известном и не изменяющемся информационном состоянии. Задача называется динамической - если информационные состояния в ходе принятия решения сменяют друг. ^ Информационные состояния ЛПР могут по-разному характеризовать его физическое состояние
Если информационное состояние состоит из единственного физического состояния, то задача называется определенной.
Если информационное состояние содержит несколько физических состояний и ЛПР кроме их множества знает еще и вероятности каждого из этих физических состояний, то задача называется стохастической (частично неопределенной).
Аналоговые модели и аналоговое моделирование При наглядном моделировании на базе представлений человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в объекте.
1) В основу гипотетического моделирования исследователем закладывается некоторая гипотеза о закономерностях протекания процесса в реальном объекте, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следстненных связях между входом и выходом изучаемого объекта. Гипотетическое моделирование используется, когда знаний об объекте недостаточно для построения формальных моделей.
2) Аналоговое моделирование основывается на применении аналогий различных уровней. Наивысшим уровнем является полная аналогия, имеющая место только для достаточно простых объектов. С усложнением объекта используют аналогии последующих уровней, когда аналоговая модель отображает несколько либо только одну сторону функционирования объекта.
С точки зрения математического описания объекта и в зависимости от его характера модели можно разделить на:
· аналоговые (непрерывные),
· цифровые (дискретные),
· аналого-цифровые (комбинированные).
Под аналоговой моделью понимается модель, которая описывается уравнениями, связывающими непрерывные величины.
Под цифровой понимают модель, которая описывается уравнениями, связывающими дискретные величины, представленные в цифровом виде.
Под аналого-цифровой понимается модель, которая может быть описана уравнениями, связывающими непрерывные и дискретные величины.
Физические модели и физическое моделирование
Физическое моделирование предусматривает воссоздание в физической модели тех же самых или аналогичных физических полей, что действуют и в объекте натуры, лишь измененных по своим абсолютным значениям в соответствии с масштабом моделирования. Одним из основных преимуществ физического моделирования является возможность осуществления прямых наблюдений за моделируемыми процессами и явлениями, иногда это преимущество является решающим. В физическом моделировании выделяется аналоговое моделирование, которое предусматривает замену в модели по сравнению с натурой одних физических полей другими, например замену натурного поля механических напряжений электрическим полем в модели или замену поля механических напряжений картиной оптической анизотропии в оптически чувствительных прозрачных материалах. Таким образом, на аналоговых моделях изучают закономерности явлений и процессов, протекающих в натурных объектах, используя математическую аналогию различных по физической природе процессов, т. е. математическую тождественность основных законов, совпадение дифференциальных уравнений, описывающих эти процессы.
Математические модели и математическое моделирование
Математическая модель (ММ) – это описание протекания процесса, описание состояния или изменения состояния системы на языке алгоритмических действий с математическими формулами и логических переходов. Кроме того, ММ допускает работы с таблицами, графиками, номограммами, выбор из совокупности процедур и элементов (последнее подразумевает использование операций предпочтения, частичной упорядоченности, включения, определение принадлежности и т.п.). Различные математические правила манипулирования со связями системы позволяют делать предсказания относительно тех изменений, которые могут произойти в исследуемых системах, когда изменяются их составляющие. Сложность формирования математической модели связана с необходимостью владения математическими методами и предметных знаний, т.е. знаний в той области, для которой создается модель. В реальности специалисту в данной практической области часто не хватает математических знаний, сведений о моделировании вообще, а для сложных задач – знания системного анализа. С другой стороны, прикладному математику трудно хорошо ориентироваться в предметной области. Следует заметить, что деление моделей на вербальные, натурно знаковые в определенной степени условно. Так, существуют смешанные типы моделей, скажем, использующие и вербальные, и знаковые построения. Можно даже утверждать, что нет знаковой модели без сопровождающей описательной – ведь любые знаки и символы необходимо пояснять словами. Часто и отнесение модели к какому-либо типу является нетривиальным.
Статические математические модели
Статистическое
моделирование представляет собой метод
получения с помощью ЭВМ статистически
данных о процессах, происходящих в
моделируемой системе.
Сущность
метода статистического моделирования
сводится к построению для процесса
функционирования исследуемой
системы S некоторого
моделирующего алгоритма, имитирующего
поведение и взаимодействие элементов
системы с учетом случайных входных
воздействий и воздействий внешней
среды E,
и реализации этого алгоритма с
использованием программно-технических
средств ЭВМ.
Теоретической
основой метода статистического
моделирования систем на ЭВМ
являются предельные
теоремы теории вероятностей.
Множества случайных явлений (событий,
величин) подчиняются определенным
закономерностям.
^ Примеры
статистического моделирования.
описывается следующими соотношениями:
![]() -
входное воздействие;
-
входное воздействие;
![]() -
воздействие внешней среды;
и
- случайные величины, для которых
известны функции распределения.
Целью
моделирования является оценка
математического ожидания М[у] величины
-
воздействие внешней среды;
и
- случайные величины, для которых
известны функции распределения.
Целью
моделирования является оценка
математического ожидания М[у] величины ![]() В
качестве оценки математического
ожидания М [у],
как следует из приведенных теорем
теории вероятностей, может выступать
среднее арифметическое, вычисленное
по формуле
В
качестве оценки математического
ожидания М [у],
как следует из приведенных теорем
теории вероятностей, может выступать
среднее арифметическое, вычисленное
по формуле
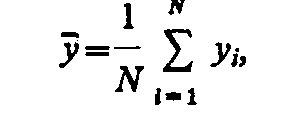 где yi — случайное
значение величины у;
N — число
реализации мат. ожиданий, которое
достаточно для статистической
устойчивости результатов.
Динамические
математические модели
где yi — случайное
значение величины у;
N — число
реализации мат. ожиданий, которое
достаточно для статистической
устойчивости результатов.
Динамические
математические модели
Динамическая математическая модель дает описание возникновения действий, которые должны сменять друг друга в известной последовательности. Чтобы модель была эффективной, ее следует механизировать, а для этого нужно установить определенный способ выполнения необходимых действий. [1]
Облегчает построение динамических математических моделей химических реакторов для выбора оптимальных пусковых и переходных режимов и для создания системы комплексной автоматизации. [2]
Детерминированнные математические модели
Теория массового обслуживания составляет один из разделов теории вероятностей. В этой теории рассматриваютсявероятностные задачи и математические модели (до этого нами рассматривались детерминированные математические модели). Напомним, что:
Детерминированная математическая модель отражает поведение объекта (системы, процесса) с позиций полной определенности в настоящем и будущем.
Вероятностная математическая модель учитывает влияние случайных факторов на поведение объекта (системы, процесса) и, следовательно, оценивает будущее с позиций вероятности тех или иных событий.
Стохастические математические модели и математические модели операций в условиях полной неопределенности
При
построении стохастических моделей её
условно представляют виде суммы
детерминированной и центрованной
составляющих,
Математические
модели исследуемых явлений или процессов
могут быть заданы в виде Таблиц,
элементами которых являются значения
частных критериев эффективности
функционирования системы, вычисленные
для каждой Принятие
решений в условиях неопределенности
Неопределенность
является характеристикой внешней среды
(природы), в которой принимается
управленческое решение о развитии:
(или функционировании) экономического
объекта. 1. Критерий Лапласа.
Этот
критерий опирается на «принцип
недостаточного основания» Лапласа,
согласно которому все состояния
«природы» ![]() ,
, ![]() полагаются
равновероятными. В соответствии с этим
принципом каждому состоянию
ставится
вероятность
полагаются
равновероятными. В соответствии с этим
принципом каждому состоянию
ставится
вероятность ![]() ,
определяемая по формуле
,
определяемая по формуле ![]() При
этом исходной может рассматриваться
задача принятия решения в условиях
риска, когда выбирается действие
При
этом исходной может рассматриваться
задача принятия решения в условиях
риска, когда выбирается действие ![]() ,
дающее наибольший ожидаемый выигрыш.
Для принятия решения для каждого
действия
вычисляют
среднее арифметическое значение
выигрыша:
,
дающее наибольший ожидаемый выигрыш.
Для принятия решения для каждого
действия
вычисляют
среднее арифметическое значение
выигрыша:
![]() Среди
Среди ![]() выбирают
максимальное значение, которое будет
соответствовать оптимальной стратегии
.
выбирают
максимальное значение, которое будет
соответствовать оптимальной стратегии
.
Оптимизационные математические модели
Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называютсяоптимизационными. Оптимизационные задачи (ОЗ) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования. Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющих эту область. Целевая функция в самом общем виде, в свою очередь, также состоит из трех элементов: управляемых переменных;
неуправляемых переменных;
формы функции (вида зависимости между ними).
Область допустимых решений это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств. Если система ограничений несовместима, то область допустимых решений является пустой. Ограничения подразделяются: а) на линейные ( ^ I и II ) и нелинейные ( III и IV ) (рис. 3.1); б) детерминированные ( А , В ) и стохастические (группы кривых С i ) (рис. 3.2).
Общая постановка задачи планирования производства |
|
Планирование является одним из наиважнейших процессов, от которого зависит эффективность деятельности компании.
Сущность этого процесса заключается в логичном определении развития предприятия, постановке целей для любого сектора деятельности и работы каждого структурного подразделения, что необходимо в современных условиях. При осуществлении планирования ставятся задачи, определяются материальные, трудовые и финансовые средства для их достижения и сроки исполнения, а также последовательность их реализации. Таким образом, можно сказать, что планирование как функция управления означает стремление учитывать заблаговременно все внешние и внутренние факторы, которые обеспечивают подходящие условия для нормального функционирования и развития предприятия.
Под экономическими ресурсами понимаются все природные, людские и производственные человеческие ресурсы, которые он (человек) применяет в хозяйственной деятельности.
Экономические ресурсы можно представить как факторы производства:
1. Земля.
2. Капитал.
3. Труд.
4. Предпринимательские способности.Любое производство обязательно требует сочетания всех четырех факторов.Экономические ресурсы ограничены, либо редки, либо невоспроизводимы, т.е. они ограничены. Необходимо при использовании экономических ресурсов обеспечивать их максимально эффективное использование.Оптимальный вариант использования экономических ресурсов — предполагает что каждая дополнительно произведенная единица продукции требует где-то сокращения производства на единицу продукции.
Основные понятия и определения в сетевых и потоковых моделях
Сетевая модель отображает взаимосвязи операций и порядок их выполнения. Операции логически упорядочены во времени в том смысле, что одни операции нельзя начать, прежде чем не будут завершены другие. Операция — это работа, для выполнения которой требуются затраты времени и ресурсов. С применением сетевых моделей решается широкий круг задач оптимизации планирования и претворения в жизнь взаимосвязанных процессов. Такие задачи возникают при осуществлении проектов любой сложности, включающих проведение некоторого комплекса мероприятий. Освоение инструмента «оптимизации на сетях» особенно актуально в связи с развитием процессного подхода к совершенствованию управленческой деятельности. Сетевые модели имеют множество модификаций. В качестве классификационных признаков используют структуру, характер информации, количество учитываемых параметров, количество выделяемых работ. По структуре сетевые модели делятся на канонические и альтернативные. Канонические модели отличаются фиксированной структурой. Это означает, что во всех вершинах над работами осуществляется единственная логическая операция В зависимости от того, какие ограничения наложены на описание событий (вершин) и операций (дуг), выделяют: сети простого типа, вершины которых не имеют внутренней структуры; иерархические сети, вершины которых рекурсивно сами обладают сетевой структурой.
Определение кратчайшего маршрута в сети
Задача поиска кратчайшего расстояния моделируется с помощью сетей или графов. К данной задаче сводятся многие задачи комбинаторной оптимизации. Существуют различные типы задач о кратчайшем пути: между двумя заданными вершинами, между заданной вершиной и всеми остальными вершинами сети, между каждой парой вершин и др.
Кратчайший путь должен быть простым, т. е. в этом пути не должны повторяться вершины и ребра сети.
Для определения кратчайшего пути помечают все вершины сети, указав в качестве начальной Vq и конечной W вершин пути первую и последнюю вершины сети.
Шаг 1. Определяются непосредственные расстояния (длиной в одно ребро) от заданной вершины Vq до всех остальных вершин.
Шаг 2. Выбирается наименьшее из них в качестве «постоянного» наименьшего расстояния (ребро между Vq и некоторой новой вершиной Уд).
Шаг 3. Это наименьшее расстояние добавляется к длинам ребер от новой вершины Уд до всех остальных связанных с нею вершин.
Шаг 4. Эта сумма сравнивается с предыдущим расстоянием от Vq до остальных вершин, и прежнее расстояние заменяется, если новое меньше.
Шаг 5. Новая вершина удаляется из списка вершин, до которых ещё не определены кратчайшие расстояния, и список укорачивается на один элемент.
Затем весь этот процесс повторяется, присоединяется новое кратчайшее расстояние к списку и т.д., пока конечная вершина не окажется соединенной с Vq путем из выделенных ребер.
Транспортная задача условие баланса транспортной задачи
Постановка
задачи. Имеется
m пунктов производства (складов)
некоторого одного продукта, задан ai –
объем производства в i-м пункте
производства, ![]() .
Есть n пунктов потребления этого
продукта, задан bj – объем потребления
(поданные заявки на поставку продукта)
в j-м пункте потребления,
.
Есть n пунктов потребления этого
продукта, задан bj – объем потребления
(поданные заявки на поставку продукта)
в j-м пункте потребления, ![]() .Пункты
производства связаны с пунктами
потребления сетью дорог с определенными
тарифами на перевозки. Стоимость
перевозки одной единицы продукта
(груза) из i –го пункта производства в
j-ый пункт потребления равна сij.
Модель. В
качестве переменных выбираются элементы
матрицы перевозок:
.Пункты
производства связаны с пунктами
потребления сетью дорог с определенными
тарифами на перевозки. Стоимость
перевозки одной единицы продукта
(груза) из i –го пункта производства в
j-ый пункт потребления равна сij.
Модель. В
качестве переменных выбираются элементы
матрицы перевозок: ![]() . Пусть
. Пусть ![]() –
количество единиц продукции, вывозимых
из i-го пункта производства в j-й пункт
потребления.
–
количество единиц продукции, вывозимых
из i-го пункта производства в j-й пункт
потребления.
 Ограничения
группы (a) задают условие: из каждого
i-го пункта производства должен быть
вывезен весь продукт. Объемы перевозок
неизвестны и составляют: х11–
количество единиц продукции, перевезенных
из первого пункта производства в первый
пукнт потебления; х12–
количество единиц продукции, перевезенных
из первого пункта производства во
второй пункт потребления; ч1n–
количество единиц продукции, перевезенных
из первого пункта производства в n-ый
пункт потребления. Сумма
всех перевезенных единиц продукции
должна быть равна a1.
Получаем ограничение:
Ограничения
группы (a) задают условие: из каждого
i-го пункта производства должен быть
вывезен весь продукт. Объемы перевозок
неизвестны и составляют: х11–
количество единиц продукции, перевезенных
из первого пункта производства в первый
пукнт потебления; х12–
количество единиц продукции, перевезенных
из первого пункта производства во
второй пункт потребления; ч1n–
количество единиц продукции, перевезенных
из первого пункта производства в n-ый
пункт потребления. Сумма
всех перевезенных единиц продукции
должна быть равна a1.
Получаем ограничение:
![]() .
.
Ограничения группы (b) задают условие: в каждый j-й пункт потребления завезен весь необходимый продукт.
Размерность
задачи: ![]() .
Транспортная задача – частный случай
задачи линейного программирования, в
которой все ограничения представлены
равенствами. В отличие от общего случая
решения задачи ЛП оптимальное решение
транспортной задачи всегда существует.
.
Транспортная задача – частный случай
задачи линейного программирования, в
которой все ограничения представлены
равенствами. В отличие от общего случая
решения задачи ЛП оптимальное решение
транспортной задачи всегда существует.
Транспортная задача с максимизацией целевой функции
Решение транспортной задачи для нахождения максимального функции Проверить задачу на сбалансированность:
составить план базисным способом северо-западного угла, рассчитать значение функции цели базисного плана;
составить базисный план методом наилучшего элемента (максимального элемента) на максимальное значение функции цели. Рассчитать функцию цели (F);
сравнить результат решения двух базисных планов;
проверить базисный план методом наилучшего элемента на максимальном значении функции цели на оптимальном потенциале и проверить улучшение плана до оптимального результата;

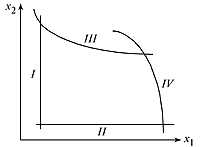 Рисунок 3.1–
Линейные и нелинейные ограничения
Рисунок 3.1–
Линейные и нелинейные ограничения  Рисунок
3.2– Детерминированные и стохастические
ограничения
Рисунок
3.2– Детерминированные и стохастические
ограничения