Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский институт управления им. П.А. Столыпина РАНХиГС (ПАГС)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЗПР, теор игр, геом метод и ТЗ(лекции мму).docx

Скачиваний:

Добавлен:

16.02.2020

Размер:

142.05 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 44

8. Методы поиска начальных и оптимальных решений транспортных задач (тз)

Алгоритм решения ТЗ,

1) находим начальное базисное допустимое (опорное) решение, состоящее из (n+m+1) заполненных клеток таблицы поставок методом северо-западного угла или методом минимальной стоимости.

2) проверяем оптимальность найденного решения (используя различные критерии оптимальности)

3) если найденное решение не оптимально, изменяем его, используя «сдвиг по циклу»: увеличиваем объём перевозок во всех нечётных клетках цикла и уменьшаем во всех чётных на величину ( равен наименьшему из объёмов перевозок в чётных клетках цикла). Переходим к пункту 2).

Построение начального решения:

В клетку (i,j) таблицы поставок вносим максимально возможный объём перевозки, равный оставшимся запасам i-го поставщика или неудовлетворённым потребностям j-го потребителя. Затем вычёркиваем из таблицы поставщика или потребителя, потребности которого полностью удовлетворены. (одна заполненная клетка таблицы – один вычеркнутый ряд матрицы).

Метод северо-западного угла: последовательно заполняем правую верхнюю клетку таблицы поставок.

Метод минимальной стоимости – в первую очередь заполняем клетки с наименьшей стоимостью перевозки.

Критерий оптимальности найденного решения в методе потенциалов.

Вычисляем потенциалы строк и столбцов матрицы поставок из уравнений , составленных для каждой заполненной клетки таблицы.

Затем, по известным потенциалам и вычисляем оценки свободных клеток:

Если все оценки свободных клеток неположительны, то найденное решение оптимально.

Переход к новому решению: Если обнаружена свободная клетка таблицы поставок, не удовлетворяющая критерию оптимальности, из неё строим цикл, вычисляем величину сдвига по циклу , если >0, осуществляем сдвиг по этому циклу и получаем новое опорное решение.

Дополнительные материалы

Двойственные задачи математического программирования.

Свойства двойственных задач.

1.) Если целевая функция одной задачи в паре стремится к минимуму, то целевая функция другой задачи стремится к максимуму.

2) Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений в другой.

3)Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.

Первая теорема двойственности:

Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение. Причём значения целевых функций этих задач на своих оптимальных решениях совпадают.

Краткие сведения из матанализа.

Функция – зависимость между числовыми величинами, при которой аргументу функции ставится в соответствие одно и только одно значение функции.

Важнейшая характеристика функции – скорость её изменения – определяется значением её производной. Производная показывает, как изменится исследуемая нами величина, при небольшом изменении переменных, от которых она зависит.

Производная функции равна конечному пределу отношения приращения функции

к приращению аргумента, когда оно стремиться к 0.

Функция возрастает, если большему значению аргумента соответствует большее значение функции.

Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Признаки монотонности Функция возрастает на тогда и только тогда, когда .

Функция убывает на , тогда и только тогда, когда

( Функция возрастает - производная положительна, функция убывает - производная отрицательна).–

Определения экстремумов

Точка -локальный максимум, если для всех точек «около» выполняется :

Точка -локальный минимум, если (эпсилон - окрестности) :

Необходимое условие экстремума

Если в точке функция достигает экстремума, то её производная в этой точке равна 0 или не существует.

Достаточные условия экстремума

Первое

Если в любой точке окрестности слева от неё производная функции положительна, а справа – отрицательна, то - локальный максимум функции.

А если производная при переходе через меняет знак с «-» на «+», то - локальный минимум.

Второе

Если в точке первая производная равна 0, а вторая производная отрицательна, то - локальный максимум функции.

Если в точке первая производная равна 0, а вторая производная положительна ,то - локальный минимум функции.

Частные производные функции двух переменных.

Частной производной по х от функции называется производная по х, вычисленная в предположении, что у – постоянная, а частной производной по у от функции называется производная по у, вычисленная в предположении, что х – постоянная.

;

Вектор градиент. Вектор, координаты которого равны частным производным функции , называется вектором градиентом этой функции. .

Определение локального экстремума функции нескольких переменных. Функция имеет локальный максимум в точке М₀(х₀,у₀), если значении функции в этой точке больше, чем её значение в любой другой точке М(х,у) некоторой окрестности точки М₀

(Точка М₀ – максимум, если для любых точек её окрестности.)

Точка М₀ – минимум, если для любых точек её окрестности.

.Необходимое и достаточное условие существования экстремума для функции двух переменных.

Необходимое: Если функция достигает экстремума в точке М₀(х₀,у₀), то все её первые частные производные в этой точке равны нулю или не существуют.

Достаточное: Пусть в некоторой окрестности точки М₀(х₀,у₀) функция имеет непрерывные частные производные, равные нулю в этой точке, тогда, если , то М₀(х₀,у₀) – является экстремумом функции , причём, если , точка М₀ – минимум, если , точка М₀ – максимум

Модель поведения потребителя.

Пусть = - набор из n товаров потребления (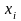 - количество i-го товара, ).

Каждый потребитель определяет для себя ценность любого набора товаров, задавая тем самым функцию потребительского предпочтения, или функцию полезности товара. .

Тогда предельная полезность i-го товара - .

Свойства функции полезности:

1)Все её первые частные производные положительны. возрастание потребления одного продукта при неизменном потреблении других приводит к росту потребительской оценки всего набора.

2) Закон Госсена. <0. предельная полезность любого товара уменьшается с ростом его потребления.

3) Смешанные частные производные второго порядка положительны. предельная полезность любого товара увеличивается с ростом потребления другого.

Линии безразличия функции полезности - линии, соединяющие потребительские наборы, имеющие один и тот же уровень полезности для потребителя. Они не имеют общих точек, не пересекаются и выпуклы вниз.

Задача потребительского выбора.

Считаясь с ограниченностью бюджета, потребитель выбирает набор товаров, приносящий ему наибольшее удовлетворение.

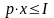, , , где -вектор цен на набор продуктов .

I – доход индивида, предназначенный для покупки набора .

- стоимость набора продуктов.

Множество наборов, стоимость которых меньше I , образуют бюджетное множество.

Оптимальное решение задачи – точка локального рыночного равновесия - лежит на границе бюджетного множества.

В точке локального рыночного равновесия предельная норма замены i-го товара j-ым равна отношению рыночных цен на эти продукты.

Вопросы к зачёту. (400)

Постановка задачи принятия управленческого решения.
Классификация ЗПР (задач принятия решения).
Структуры и этапы исследования ЗПР.
Выработка решения в условиях риска. Критерий ожидаемого выигрыша.
Критерии минимизации рисков в ЗПР.
Критерии принятия решения в условиях неопределённости.
Определение и общая постановка задачи теории игр.
Понятие чистой и смешанной стратегии. Платёжная матрица.
Критерий существования решения игры в чистых стратегиях. Седловая точка.
Критерий Вальда. Верхняя и нижняя цена игры. Вычёркивание доминируемых(щих) рядов.
Понятие смешанной и активной стратегии. Теоремы Неймана и об активной стратегии.
Постановка задачи математического программирования.
Постановка задачи МП, решаемой графическим методом. Построение ОДР (области допустимых решений)
Понятие линии уровня и вектора градиента. Построение опорной прямой и поиск оптимального решения.
Постановка и основные понятия транспортной задачи.
Алгоритм решения транспортной задачи. Понятие цикла.
Методы нахождения начального решения транспортной задачи.
Критерий оптимальности решения ТЗ, переход к новому решению.
Двойственные задачи математического программирования.
Задача потребительского выбора.

Контрольные работы. (600)

Поиск управленческого решения в условиях риска. (70)
Поиск управленческого решения в условиях неопределённости.(80)
Решение игры в чистых стратегиях. (50)
Поиск решения игры в смешанных стратегиях (80)
Построение ОДР и опорных прямых в задачах ЛП. (50)
Решение двумерной ЗЛП графическим методом. (100)
Поиск начального решения транспортной задачи. (50)
Решение ТЗ с неправильным балансом методом потенциалов.(120)

Зачёт. Два теоретических вопроса по 150 баллов и практическое задание на 100 баллов (максимум 400 баллов)

850 баллов и выше - отлично

С 720 баллов - хорошо

С 600 баллов - удовлетворительно