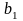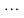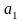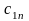- •1. Системный подход к задачам принятия управленческого решения.
- •2. Выработка решения в условиях риска.
- •3. Критерии принятия решения в условиях неопределённости.
- •4. Основные понятия теории игр.
- •5. Постановка задачи мп.
- •6. Геометрическое решение задач математического программирования.
- •7. Постановка и основные понятия транспортной задачи.
- •8. Методы поиска начальных и оптимальных решений транспортных задач (тз)
5. Постановка задачи мп.
Операция – управляемое мероприятие, направленное на достижение цели.
Условие задачи математического программирования состоит из:
(1)
 =
= целевой функции,
характеризующей зависимость
целевой функции,
характеризующей зависимость
результата операций от её факторов, переменных ЗМП.
(2)

 системы ограничений, состоящей
из m
равенств или неравенств,
системы ограничений, состоящей
из m
равенств или неравенств,

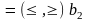 показывающей
связи
между факторами
операции,
показывающей
связи
между факторами
операции,
…


Допустимое
решение ЗМП
- любой n-мерный
вектор
 удовлетворюящий
системе ограничений (2) и естественному
условию неотрицательности переменных
удовлетворюящий
системе ограничений (2) и естественному
условию неотрицательности переменных
Совокупность всех допустимых решений образуют область в n-мерном пространстве – ОДР.
Решить ЗМП – выбрать из всех допустимых решений то, при котором результат операции будет наилучшим (целевая функция (1) достигнет своего наибольшего или наименьшего значения).
Оптимальным решением ЗМП называется допустимое решение ЗМП, при котором целевая функция = достигает экстремума.
6. Геометрическое решение задач математического программирования.
Рассмотрим ЗМП с двумя неизвестными:

 -
целевая функция
-
целевая функция
 - система ограничений
- система ограничений
1) Строим ОДР задачи.
Областью
решения каждого из неравенств
 будет
часть плоскости, ограниченная линией
будет
часть плоскости, ограниченная линией .
Очевидно, что решением системы неравенств
будет пересечение всех их областей
решений.
.
Очевидно, что решением системы неравенств
будет пересечение всех их областей
решений.
 ОДР
задачи МП – общая часть областей решений
всех неравенств системы ограничений.
ОДР
задачи МП – общая часть областей решений
всех неравенств системы ограничений.
Если ОДР – пустое множество, задача не имеет решения в силу несовместности системы ограничений.
Если ОДР – непустое множество, задача имеет одно или бесконечное множество решений.
2) Строим линии уровня целевой функции (линии, в которых значение функции постоянно).
=С –уравнения линий уровня.
Если Z – линейная функция, то её линии уровня – семейство прямых, перпендикулярных вектору градиенту этой функции.
Вектором
градиентом
функции
называется
вектор ,
координаты которого равны частным
производным этой функции.
,
координаты которого равны частным
производным этой функции.
3) Двигаясь от одной линии уровня к другой в направлении вектора градиента (в задачах на максимум) или в противоположном направлении (в задачах на минимум), находим опорную кривую.
Опорная кривая _ такая линия уровня, которая имеет хотя бы одну общую точку с ОДР, и, при этом, не разделяет её на части.
4) Находим оптимальное решение задачи – общие точки ОДР и опорной кривой.
7. Постановка и основные понятия транспортной задачи.
Дано:
Несколько (m)
поставщиков однородного товара хотят
передать этот товар нескольким (n)
потребителям. Мощность
i
го поставщика
 -
равна запасам товара у этого поставщика.
Мощности поставщиков заносятся в первый
столбец таблицы поставок. Мощность
j-го
потребителя -
-
равна запасам товара у этого поставщика.
Мощности поставщиков заносятся в первый
столбец таблицы поставок. Мощность
j-го
потребителя - -
определяется количеством необходимого
ему товара. Мощности потребителей равны
их запросам. Известна стоимость перевозки
единицы товара от каждого из поставщиков
к каждому потребителю -
-
определяется количеством необходимого
ему товара. Мощности потребителей равны
их запросам. Известна стоимость перевозки
единицы товара от каждого из поставщиков
к каждому потребителю -
 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
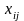 ,
то есть составить оптимальный
план
перевозок товара. при котором:
,
то есть составить оптимальный
план
перевозок товара. при котором:
суммарные затраты на перевозку будут минимальными;
|
2)мощности всех поставщиков реализованы; 3) запросы всех потребителей удовлетворены
:


Необходимое и достаточное условие существования решения транспортной задачи.
Суммарные запасы поставщиков и потребителей равны между собой.
Цикл клетки (i,j) – последовательность клеток таблицы ТЗ, определяемая ломаной линией, состоящей из вертикальных и горизонтальных звеньев. Начало и конец ломаной – в клетке (i,j), остальные вершины – в заполненных клетках таблицы.
Допустимое решение ТЗ является базисным тогда и только тогда, когда из заполненных им клеток таблицы нельзя образовать ни одного цикла.