3. Расчет балки перекрытия
Исходные данные:
По заданию на проектирование:
Постоянная нагрузка от веса конструкций пола и перегородок gn,n =3,5 кН/м² (нормативная нагрузка от перегородок равна 2,5 кН/м², нагрузку от конструкций пола принимаем равной 1 кН/м²)
Временная нормативная нагрузка νn = 4,5 кН/м²
Коэффициент надежности по ответственности здания II уровня γn = 0,95.
Условия эксплуатации – закрытое помещение при нормальной влажности воздуха.
Бетон тяжелый класса В20.
Класс продольной рабочей арматуры: А400, поперечной – А240
По результатам выполнения п.1 и 2
Пролет балок lb = 6,0м.
Расстояния между балками в осях lo1 = lo2 = 2,4м.
Толщина плиты hp =70 мм.
3.1. Расчетные характеристики материалов и коэффициенты.
Бетон балки перекрытия тот же, что и в плите, то есть тяжелый класса В20. К уже известным его расчетным характеристикам добавляется
Rbt = γb1×Rbt(табл),
Rbt = 0,9·0,9 =0,81 МПа,
где Rbt –расчетное сопротивление бетона осевому растяжению с учетом коэффициента γ bl =0,90.
Для арматуры из стали класса А400, расчетное сопротивление арматуры на растяжение Rs = 355 МПа, а для поперечной – Rsw = 170 МПа.
Для расчета на усилия, возникающие от действия изгибающего момента
,
где l – расстояние между разбивочными осями,
lon – размер опирания балки на стену,
b01,b02 – привязки стен к разбивочным осям.
Для расчета по наклонным сечениям (на действие поперечной силы)
lbl = l – (b01+b02),
где lbl – пролет балки в свету
lbl = 6,0 – (0,19 + 0,19) = 5,61 м
3.2.Определение расчетных нагрузок на балку.
а) Постоянная, равномерно
распределенная нагрузка ( с
и с γn
=0,95):
Поскольку, фактическая высота плиты совпала с принятой ранее при расчете нагрузок на плиту, то нагрузку от плиты не уточняем, принимая ее равной:g0 =5,75кН/м²
Расчетная погонная нагрузка от собственного веса ребра балки, расположенного ниже плиты
Итого постоянная расчетная погонная нагрузка на балку:
б) Временная нагрузка ( с учетом γfν = 1,2, γn =0,95, νn =2,0 кН /м):
qp =γn · γfv · νn · l02
qp = 0.95 ·1,2 ·4,5 · 2,4 = 12,3 кН /м
в) Полная расчетная погонная нагрузка
q= qg +qp
q = 15,35 + 12,3 = 27,65 кН /м
3.3.Выбор расчетной схемы и статический расчет.
Принимаем расчетную схему в виде однопролетной статически определимой балки и получим расчетные усилия
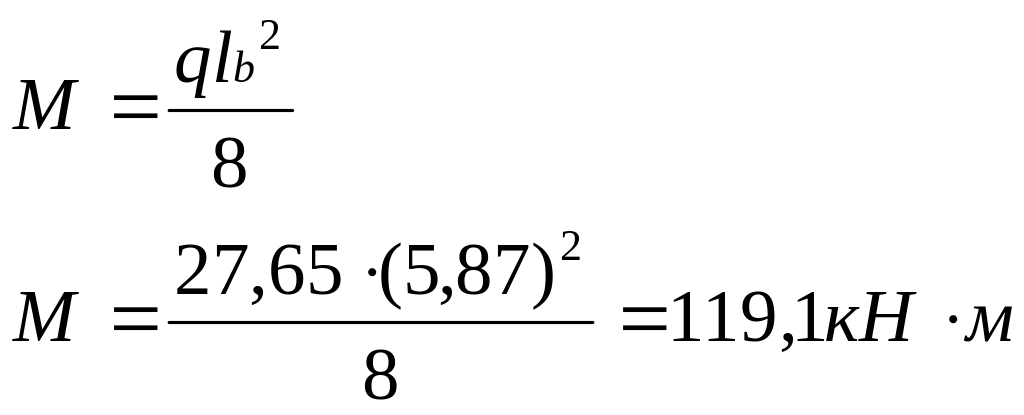
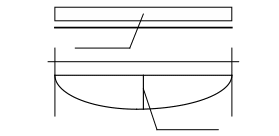
q=27,65 кН /м
l
b
= 5,87 м
М= 119,1 кН · м
Рис.3.1. Расчетная схема и расчетные усилия для расчета на прочность по нормальным сечениям.
3.4. Расчет балки по сечениям, нормальным к продольной оси.
3.4.1. Определение высоты сечения балки.
Принимаем ξ =0,40, а b = 200 мм; тогда:
αm= ξ(1 – 0,5ξ)
αm = 0,4(1 – 0,5 ∙ 0,4) = 0,32.
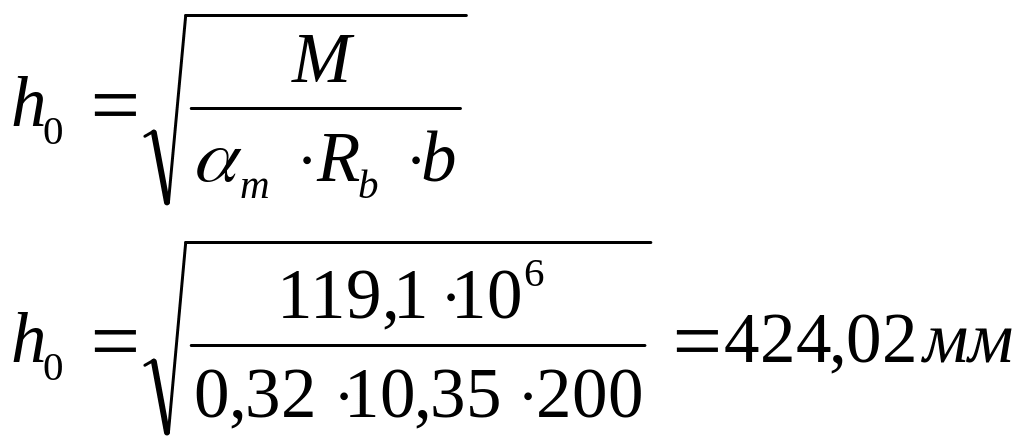
Требуемая высота поперечного сечения балки
hmp = h0 + a, а = 65 мм
hmp = 424,02 + 65 = 489,02 мм
Окончательно принимаем высоту балки h = 500 мм. Отношение h/b = 500/200 = 2,5 находится в рекомендуемом диапазоне: hb = (1/11÷1/15)lb; bb = (0,3÷0,6) hb =>. hb/bb = (1,6÷3,3)
3.4.2. Определение продольной арматуры.
Сечение балки тавровое с полкой, расположенной в сжатой зоне.
Высота и ширина полки определяются из условий:
h'f = hp = 70 мм > 0.1h = 0,1 ∙ 500 = 50 мм
b'f = 0,5 ∙ l1 ∙ 2 + b(теоретический расчет), где l1 – расстояние между балками в свету,
l1 = l02 – b, b = 200 мм,
l1 = 2400 – 200 = 2200 мм
b'f = 0,5 ∙ 2200 ∙ 2 + 200 = 2400 мм
b'f = 2 ∙ lb/6 + b (экспериментальная формула)
b'f = 2 ∙ 5870/6 + 200 = 2156,66 мм
Принимаем b'f = 2100 мм (наименьшее значение)
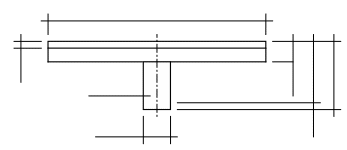
Рис.3.2 Расчетное сечение балки.
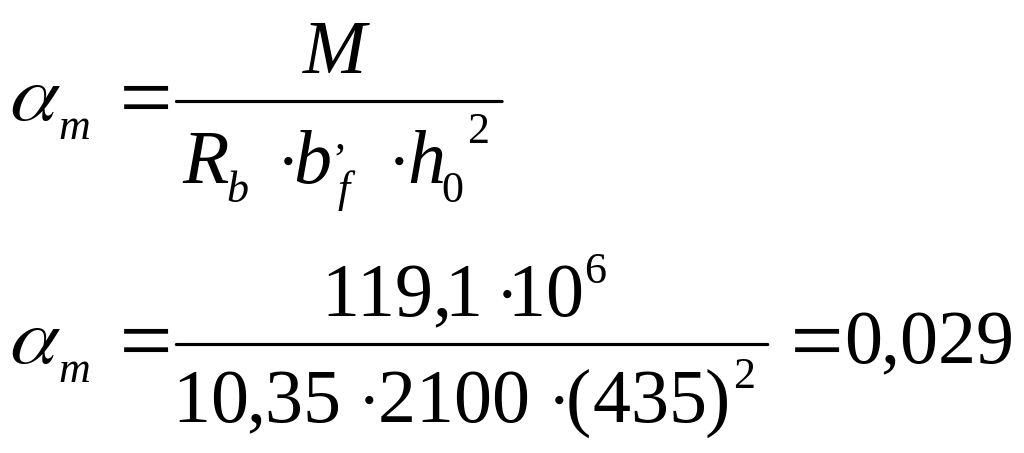
ξ =
ξ =
х=ξ·h0
х = 0,029 ·435 = 12,62 мм < hf = 70мм, т.е. нейтральная ось действительно находится в полке.
Площадь сечения арматуры определяем по формуле
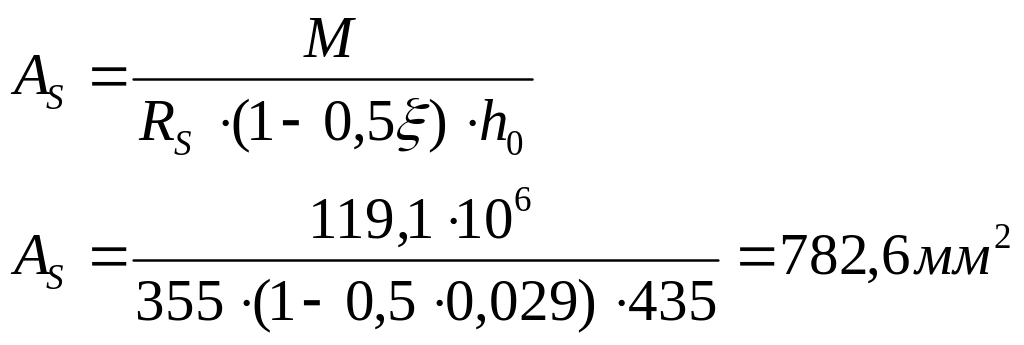
Принимаем 2 Ø 25 А400 c АSreal = 982 мм2.
Фактический коэффициент армирования равен
,
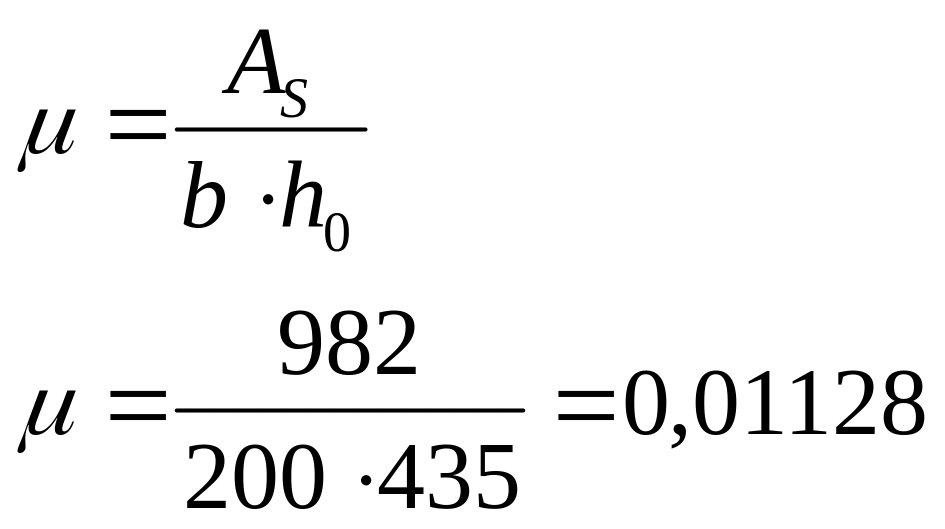а процент армирования μ% =1,13 % > μmin =0,10%
Уточняем h0 по принятым диаметрам продольной арматуры. При арматуре Ø 25 мм расстояние от крайнего растянутого волокна до центра тяжести площади сечения растянутой рабочей арматуры равно a = 70 мм.[10, табл. Б.1, прил. Б] Тогда
h0 = h – a
h0 = 500 – 70 = 430 мм.
Этот размер принимаем для дальнейших расчетов и конструирования.