Упражнение 8.3. Система с потерями м/е2/2

Рассмотрим систему с потерями с двумя каналами (обслуживающие приборы). Попытки вызова прибывают согласно Пуассоновскому про­цессу интенсивностью X вызовов в единицу времени. Время обслужи­вания X распределено в соответствии с Эрланговским распределением с интенсивностью 2(Х в каждой из этих двух фаз.

1. Найти предложенную нагрузку.

2. 3. Найти согласно предположению о статистическом равновесии веро­ятности состояний системы, используя тот факт, что усеченное

   Создать диаграмму переходов состояний системы, где состояние обозначает число вызовов в системе и фазы вызовов. Примените следующее состояния, где а и b обозначают эти две фазы.

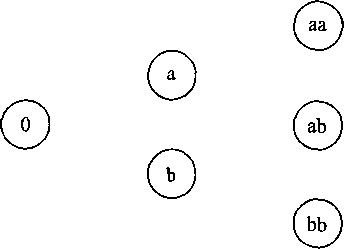
Пуассоновское распределение для данного среднего времени пре­бывания в системе справедливо для любого распределения времени обслуживания (свойство нечувствительности).

4. Блокирующее состояние «оба канала заняты» инициируется из состоя­ния а или Ь. Определите для обоих из этих случаев распределение Кокса и продолжительности блокирующего состояния, применяя графиче­ское представление распределения Кокса (диаграмму состояний).

5. Записать преобразования Лапласа из распределения продолжитель­ности периодов, когда оба канала заняты.

6. Найти среднюю величину и дисперсию числа попыток вызова, кото­рые блокированы в течение периода, когда оба канала а и b заняты.

Упражнение 8.9. Энегсетовская система с потерями

Мы рассматриваем Энгсетовскую систему с потерями с 3 серверами, у которых предложенная нагрузка производится из 4 однородных источ­ников. Свободный источник генерирует вызовы с интенсивностью у = Уг [вызов/единица времениJ, и время обслуживания является экспоненциаль­но распределенным со средней величиной ц*¹ = 1 [единица времени].

1. Найти полную предложенную нагрузку от этих 4 источников.

2. Установить диаграмму переходов состояний и найти вероятности состояния согласно предположению о статистическом равновесии.

3. Найти потери по времени, потери по вызовам и потери по нагрузке, используя следствия вопросов 1 и 2.

4. Найти распределение (плотность распределения) числа вызовов, кото­рые блокированы в течение периода, когда все три сервера заняты.

5. Получить вероятности состояния системы свертыванием вероятно­сти состояния 4 единственных источников и сделать сечение вероят­ности состояния в состоянии 3.

Упражнение 8.10. Система с потерями и интенсивностью прибытия, зависящей от состояния

Мы рассматриваем систему с потерями с п = 2 каналами. Состояние системы / определяется как число занятых каналов. Заявки от клиентов прибывают согласно Пуассоновскому процессу с интенсивностью, зави­сящей от состояния.

3. — i

y(i) = ——. • у [заявок в единицу времени], 0 < i < 3.

Для всех других состояний у(/) = 0.. Мы выбираем у = 1 заявки в еди­ницу времени, а время обслуживания - экспоненциально распределенное с интенсивностью ц, = 1 заявок в единицу времени.

1. Создать диаграмму переходов состояний системы.

2. Найти вероятности состояния системы согласно предположению о статистическом равновесии и определить потери по времени Е.

3. Найти вероятности состояния л(/), как они выполняются при произ­вольном поступлении вызовов, и найти потери по вызовам В.

4. Найти предложенную нагрузку, определенную как нагрузка, которая будет обслужена в системе без потерь, и найти потери по нагрузке С.

5. Принять, что оба канала заняты. Какова вероятность, что следую­щее событие - попытка вызова (который, конечно, будет потерян)? Найти распределение числа вызовов, которые будут потеряны в тече­ние периода занятости.

6. Дать вероятности состояния, как они замечены клиентом, который только что отбыл от системы. Мы включаем клиентов, которые бло­кированы.

Упражнение 8.11. Модель АЛОХАа с Энгсетовской нагрузкой

Мы рассматриваем Энгсетовскую модель с S = 4 источниками. Среднее время пребывания в системе выбрано как единица времени (цг¹ = 1). Интенсивность поступления свободного источника - у = Уз. Оба временных интервала являются экспоненциально распределенными. Число каналов бесконечно, то есть п < S. Состояние системы определено

как число занятых каналов. Вышеупомянутая система — модель несин­хронной системы AJTOXAa с S передатчиками и экспоненциально распре­деленными длинами пакета.

1. Найти предложенную нагрузку А.

2. Создать диаграмму переходов состояний и найти согласно пред­положению о статистическом равновесии вероятности состояния р (/), (/' = 0, 1, ..., 4).

3. Найти вероятности состояния n(i), (/ = 0, 1,..., 4), как они наблюдают­ся поступающим вызовом, перед поступлением (математические ожи­дания вызова). Используйте, как отправную точку, либо вероятности состояния, которые получены в вопросе 2, либо теорему прибытия.

4. Какова вероятность того, что вызов, прибывающий в нулевом состо­янии (и, таким образом, изменяющий состояние из состояния нуль в состояние один), завершит обслуживание прежде, чем поступит следующий вызов? Это соответствует успешной передаче вызова в протоколе AJIOXAa.

5. Каково среднее время пребывания в системе успешно обслуженного вызова?