2. М/м/п система организации очереди

Мы можем также получить рассмотренные выше результаты для системы с п обслуживающими приборами. Для (i+j)<n получаем ту же самую вероятность относительного состояния, что и для многоразмерной В-формулы Эрланга. Для (i+j)>rt получаем решение только для простого случая, когда ц. = |1, то есть когда все типы (цепочки) клиентов имеют одно и то же среднее время пребывания в системе. Мы тогда находим вероятности состояния, данные в (10.9), и система имеет мультиплика­тивную форму. М/М/1 можно рассматривать как частный случай М/М/п и по аналогии с системами с потерями (лекция 12).

3. Закрытые сети очередей с несколькими цепочками

Рассмотрение сетей очередей, имеющих много цепочек, аналогично случаю с единственной цепочкой. Основное различие состоит в том, что классическая формула и алгоритмы заменены соответствующей много­мерной формулой.

1. Алгоритм свертывания

Алгоритм по существу такой же, как и в случае единственной цепочки.

• к

  

  Шаг 1. Рассмотрим каждую цепочку так, как будто она является единственной в сети. Найдите относительную нагрузку в каждом узле, решая уравнения равновесия потока (14.5). В произвольном опорном узле принимаем, что нагрузка равна единице. Для каждой цепочки мы можем выбрать в качестве опорного узла свой узел. Для цепочки j в узле к относи­тельная интенсивность прибытия У_к (используем верхний индекс, чтобы указать номер цепочки) получается из: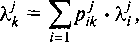

(14.17)

где:

К — число узлов,

N — число цепочек,

р>._к — вероятность, что клиент цепочки j перейдет с узла i к узлу к.

Мы выбираем произвольный узел как опорный узел, например узел 1, то есть А/, = 1. Относительная нагрузка в узле к клиентов цепочки j

тогда:

где s^J_t — среднее время обслуживания в узле к для клиентов цепочки j. Обратите внимание, что j — индекс, а не степень.

• Шаг 2. На основе значений относительных нагрузок, найденных на шаге 1, мы получаем многомерные вероятности состояния для каждого узла. Каждый узел рассматривается отдельно. Далее, усекаем простран­ство состояний согласно числу клиентов в каждой цепочке. Например, для узла к (\<к<К)\

где S — число заявок от клиентов в цепочке j.

• Шаг 3. Чтобы найти вероятности состояния полной сети, сверты­ваем вероятности состояния каждого узла подобно случаю единственной цепочки, - разница в том, что в данном случае свертывание многомерно. Когда выполним последнее свертывание, получим критерии качества работы последнего узла. Снова изменяя порядок узлов, мы можем полу­чить критерии качества работы всех узлов.

Общее количество состояний увеличивается быстро. Например, если цепочка j имеет S заявок клиентов, то общее количество состояния в каж­дом узле становится:

N

Пути N цепей с S. заявками в цепи j могут быть распределены в сети очередей с К узлами:

N

(14.18)

С =\{C(Sj,kj

Sj +kj - 1 kj - 1

- 1

Sj + kj — 1

Sj

(14.19)

C(Sj,kj) =

Алгоритм лучше всего проиллюстрировать примером.

где k.( 1 < к<К) - номер узлов, посещенных клиентом в цепи у, и: