1. Всмр-сети очередей

В 1975 г. вторая модель Джексона была далее обобщена Baskett, Chandy, Muntz и Palacios (1975 [4]). Они показали, что сети очередей с более чем одним типом клиентов также имеют мультипликативную форму, при условии, что:

а) каждый узел имеет симметричную систему организации очереди (см. секцию 14.2: Пуассоновский поток вызовов —> Пуассоновский процесс освобождения);

б) заявки от клиентов классифицированы в N цепочки. Каждая цепочка характеризуется своим собственным средним временем обслужи­вания 5. и вероятностями перехода р_и Кроме того, после окончания обслуживания в узле клиент может переходить из одной цепочки к другой с некоторой вероятностью. Имеется одно ограничение: если дисциплина организации очереди в узле — М/М/п (включая М/М/1), то среднее время обслуживания должно быть идентично для всех цепо­чек в узле.

ВСМР-сети могут быть рассчитаны с помощью многомерного алго­ритма свертывания и многомерного Л//01-алгоритма.

Смешанные сети очередей (открытые и закрытые) рассчитываются сначала путем вычисления нагрузки от открытых цепочек в каждом узле. Эту нагрузку нужно обслуживать так, чтобы соблюдалось статистическое равновесие.

Производительность этих узлов уменьшается на эту нагрузку, и закрытая сеть очередей рассчитывается уже с меньшей производитель­ностью. Так что главная проблема состоит в расчете закрытых сетей. Для этого мы можем использовать много алгоритмов, среди которых самыми важными являются алгоритмы свертывания и Алгоритм Средней величины (MVA - Mean Value Algorithm).

2. Многомерные сети очередей

В этой секции мы рассматриваем сети очередей с более чем одним типом клиентов. Клиенты одного и того же типа принадлежат заданному классу или цепочке. В лекции 10 мы рассматривали системы с потерями, обслуживающие несколько типов клиентов (услуг), и замечали, что может быть получена мультипликативная форма и может быть применен алго­ритм свертывания.

1. М/м/1-система организации очереди с одним обслуживающим прибором

Рис. 14.7 иллюстрирует систему организации очереди с одним обслу­живающим прибором и с N = 2 типа заявок от клиентов (цепочек). Заявки от клиентов прибывают в систему согласно Пуассоновскому потоку вызо­вов с интенсивностью X (/ = 1, 2). Состояние (i,j) определено как состоя­ние / заявок клиента типа 1 и j заявок от клиента типа 2. Интенсивность обслуживания ц. в состоянии (/, j) может быть выбрана зависящей от состояния, например:

^ ⁼ 7ТГ^ ⁺ 7Т7'^Ц2-

Интенсивности обслуживания могут интерпретироваться несколь­кими способами, но они должны соответствовать симметричной системе организации очереди при наличии одного обслуживающего прибора.

Одна из интерпретаций соответствует совместному использованию процессора, то есть все (/ + j) клиентов совместно используют обслужи­вающий прибор, а производительность сервера является постоянной. Зависимость состояния от типа клиента происходит из-за разности в интенсивности обслуживания двух типов клиентов. То есть число заявок от клиентов, покидающих систему, в единицу времени зависит от типа клиентов, обслуживаемых в настоящее время.

Можно показать, что обслуживаемая заявка с вероятностью i/{i+j) принадлежит к типу 1 и с вероятностью j/(i +J) — к типу 2 независимо от дисциплины обслуживания.

Рис. 14.8 дает часть диаграммы переходов состояний. Диаграмма обратима, так как поток по часовой стрелке равняется потоку против часовой стрелки. Следовательно, есть местное равновесие, и все вероят­ности состояния могут быть выражены с помощью р(О, 0):

Рисунок 14.7. Af/jty/7-система организации очереди с двумя типами (цепочками) клиентов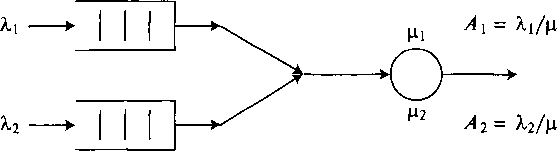

Рисунок 14.8. Диаграмма переходов состояний для многомерной системы М/М/1 с совместным использованием процессора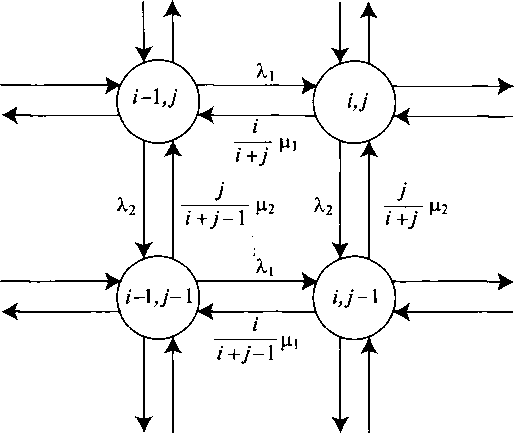

(14.14)

P(U) = ^t-^f-U+jy.-P(0,0).

I- у!

Используя нормализацию, получаем р(0, 0):

00 00

ILILpVJ) = 1 •

1=0 7=0

По сравнению с многомерной В-формулой Эрланга, здесь суще­ствует дополнительный коэффициент (/+/)!. Мультипликативная форма выражения между цепочками (на узле) потеряна, но мультипликативная форма между узлами все еще поддерживается.

Примем, что есть N различных типов клиентов (цепочек) вероятно­сти состояния для единственного узла, и получаем:

Р(0 = P(iu h, {iK j

L y=i

[ff

U=i

( N 'I

■Р( 0). (14.15)

Это может быть выражено полиномиальным распределением (4.37):

/i + h + ‘' + ‘n

/ь h, • ■ ■ ,lN

(14.16)

•Р(

0).

мо - {ГК} • (

Для бесконечного числа мест ожидания вероятности состояния общего количества клиентов:

p(j)=p{i 1 + h + ••• + h =j} ■

Если ц. = (д., то система идентична Л//М//-системе с интенсивностью поступления X = £ А,,-:

pU) - (А\+А_г +■■■ + A_Ny-р^) = A^j - (I-А) .

Чтобы получить этот результат, используется биноминальное разло­жение. Диаграмма переходов состояний на рис. 14.8 может также интерпре­тироваться как диаграмма переходов состояний системы M/G/1-LCFS-PR (приоритетное возвращение к работе). Очевидно, что M/G/1-LCFS-PR обратимо, потому что процесс в диаграмме переходов состояний проходит одинаково как вперед из нуля, так и назад, чтобы вернуться в нуль.

Можно показать, что диаграмма переходов состояний нечувстви­тельна к распределению времени обслуживания, так что она справедлива для системы организации очереди М/G/l. Рис. 14.8 соответствует диаграмме переходов состояний для системы организации очереди с одним обслужи­вающим прибором и гиперэкспоненциально распределенными времена­ми обслуживания (см. (10.7)), например. M/H₂/l-LCFS-PR или PS.

Заметим, что для M/M/1 (FCFS, LCFS, SIRO) необходимо, чтобы все клиенты имели одно и то же среднее время обслуживания, которое долж­но быть экспоненциально распределенным. Другими словами, обслу­живаемый клиент не будет случайным клиентом среди (/+/) клиентов в системе.

В заключение заметим, что системы организации очереди с одним обслуживающим прибором и большим количеством типов клиентов будут иметь мультипликативную форму только тогда, когда узел имеет симме­тричную систему организации очереди: M/G/l-PS, M/G/1-LCFS -PR или М/М/1 с одним и тем же временем обслуживания для всех клиентов.