1. Исторические замечания по m/d/n

Системы организации очереди с Пуассоновским потоком вызовов и постоянными временами обслуживания были проанализированы пер­выми. Интуитивно можно было бы думать, что анализ более систем с постоянными временами обслуживания проще, чем с экспоненциально распределенными временами обслуживания, но это явно не так. С экспо­ненциальным распределением иметь дело проще из-за отсутствия у него памяти: остающееся время «жизни» имеет то же самое распределение, как полное время «жизни» (секция 4.1), и поэтому мы можем забыть о периоде или моменте времени, когда начинается время обслуживания. Постоянные времена занятия требуют, чтобы мы помнили точное время начала. Эрланг первым проанализировал систему с постоянным временем обслуживания M/D/n, FCFS (Brockmeyer, 1948 [11]):

Эрланг: 1909 п = 1 ошибка для п> 1,

Эрланг: 1917 п = 1, 2, 3 без доказательства,

Эрланг: 1920 п - произвольное, решения для п = 1, 2, 3.

Эрланг получил распределение времени ожидания, но не рассма­тривал вероятности состояния. Фрей (Fry (1928 [30])) также исследовал М/D/l и получил вероятности состояния (уравнения состояния Фрея), используя принцип статистического равновесия Эрланга. Сам Эрланг применял другие теоретические методы.

Кроммелин (1932 [20], 1934 [21]), британский телефонный инженер, представил общее решение для M/D/n. Он обобщил уравнения состояний Фрея для произвольного п, и получил распределение времени ожидания, теперь называемое распределением Кроммелина.

Поллячек (1930-34) представил общее, зависимое от времени посту­пления решение для произвольного распределения времени обслужива­ния. Согласно предположению о статистическом равновесии он получил явные решения для экспоненциально распределенного и постоянного времен обслуживания.

Хинчин (1932 [63]) исследовал M/D/n и получил распределение вре­мени ожидания.

2. Вероятности состояния m/d/1

Вероятности состояний для М/D/l могут быть получены простым способом, исходя из предположения о статистическом равновесии.

Пусть интенсивность поступления вызовов равна X, а постоянное время занятия — h. Рассматриваем чистую систему с ожиданием и с един­ственным обслуживающим прибором.

Предложенная нагрузка = Обслуженная нагрузка = X - h < I, (13.39) то есть

А = Y=X-h = 1 - /7(0),

в каждом состоянии, кроме нулевого, обслуженная нагрузка равна 1 Эрл.

Мы рассматриваем два периода (момента времени) t и t + h на рас­стоянии h. Каждый клиент, обслуживаемый в период t (самое большее один период), может покинуть обслуживающий прибор в период t+h. Клиенты, прибывающие в течение интервала (/, t + h), находятся все еще в очереди в период t+h (ожидание или обслуживание).

Процесс поступления вызовов — Пуассоновский процесс. Следовательно, мы имеем Пуассоновское распределение прибытия во временном интервале (/, t+h):

(XhV

p(j> h) — p{j calls in A} = —— • e , j =0,1,2.... (13.40)

Вероятность того, что данное состояние в период t+h может быть получено из состояния в период t, определяется, принимая во внима­ние общее количество вызовов и выходы из состояния в течение (t, t+h). Рассматривая эти периоды, получаем марковскую цепь, внедренную в первоначальный процесс обслуживания нагрузки (рис. 13.4).

Мы получаем уравнения состояний Фрея для п = 1 (Fry, 1928 [30]):

p(j, h) = p{j calls in h) = • е~^ЯЛ , j = 0,1,2... .

J'- (13.40)

Выше было установлено:

/>(0) = 1 -A

и согласно предположению о статистическом равновесии p_t(i) = p_l+h(i), мы последовательно находим:

р( 1) = (1 1} ,

р{2) = (1 - А)-{-е*-(1 + А) + е^и} ,

и далее

Pd) = A)e^JA• ■ ^ }, i-2,3,... (13.42)

Последнее слагаемое, соответствующее j=i, всегда равняется с'^А, ПОСКОЛЬКУ (-1)! S оо.

Состояние Поступление в (Л t+h)

Состояние

Рисунок 13.4. Иллюстрация уравнений состояния Фрея для системы организации очереди M/D/1

3. Средние времена ожидания и период занятости M/D/1

Для Пуассоновского процесса поступления вызовов вероятность задержки D равна вероятности того, что он не находится в нулевом состо­янии (свойство PASTA):

D = A = l-p(0). (13.43)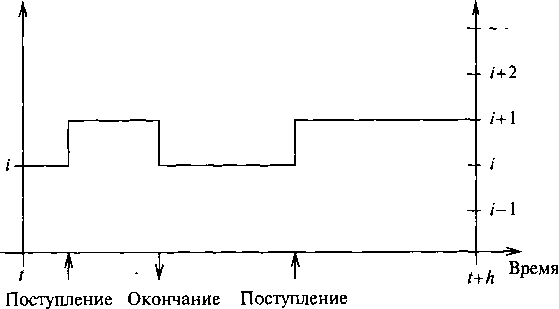

В принципе р(0) может быть получено из условия, что все вероятно­сти состояния должны в сумме давать единицу.

W обозначает среднее время ожидания для всех клиентов, и w обо­значает среднее время ожидания для клиентов, которые стоят в очереди (положительное значение времени ожидания). Мы имеем для любой системы организации очереди (3.20):

W

w =£. (13.44)

W и w могут быть легко получены, используя формулу Поллячека- Хинчина (13.2):

W =

А ■ h

2(1 - А) ’ (13.45)

w =

h

2(1 -А) (13.46)

Средняя величина периода занятости была получена для M/G/1 в (13.7) и иллюстрирована для постоянных времен обслуживания на рис. 13.1:

т_г, = (1317)

Среднее время ожидания для задержанных клиентов, таким обра­зом, — половина периода занятости. Это показывает, что вызовы от кли­ентов прибывают случайно в течение периода занятости, но мы знаем, что ни один вызов не поступает в течение последнего времени обслуживания периода занятости.

Можно показать, что распределение числа вызовов, прибывающих в течение периода занятости, можно выразить распределением Борет (Borel):

B(i)= i= 1,2,... (13.48)

4. Распределение времени ожидания: M/D/1, FCFS

Можно показать, что:

p{W< t) =1 - (1 - X) • Z —'ⁱ~—.'!,^Г+У • е~^хи~^г), (13.49)

7 = 1

(T+j)\

где h=1 выбрано как единица времени, t=T+x, Т — целое число, и 0<т<1.

Граф распределения времени ожидания имеет нарушения каждый раз, когда время ожидания превышает кратное число постоянного време­ни занятия. Пример для распределения вероятности дополнения времени ожидания (р(W> t)) показан на рис. 13.5.

Рисунок 13.5. Распределение дополнения времени ожидания для всех клиентов в системе организации очереди М/М/1 и М/D/l для дисциплины очереди (FCFS). Единица времени = среднее время обслуживания. Заметим, что среднее время ожидания для М/D/l — только половина времени для М/М/1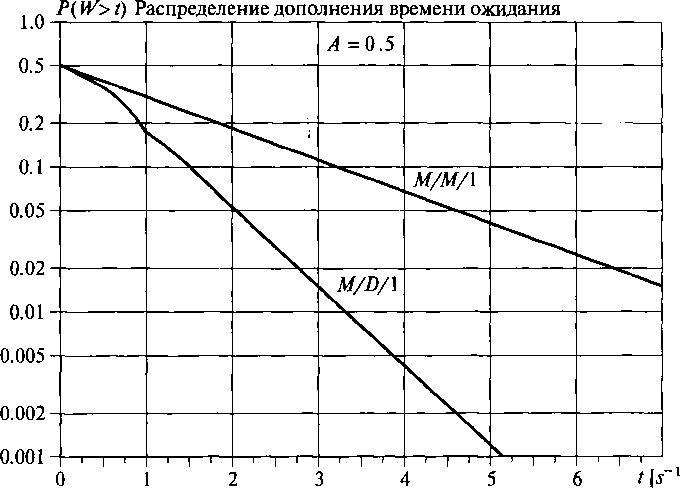

Формула (13.49) неудобна для числовой оценки. Можно показать (Iversen, 1982 [39]), что формула времени ожидания может быть записана в более компактной форме, например, введенной Эрлангом в 1909 г.:

т

p{W< /} = (I - ~ -■е~¹¹'-^,), (13.50)

j=o У!

и может применяться для числовой оценки при малых временах ожи­дания.

Для больших времен ожидания мы обычно интересуемся составны­ми значениями t. Можно показать (Iversen, 1982 [39]), что для составного значения V.

р{ W < /} = р(0) + р(1) + • • • + p{t). (13.51)

Вероятности состояния p(i) вычисляются наиболее точно, с помо­щью рекурсивной формулы, основанной на уравнениях состояний (13,42) Фрея:

P(i+\) = jj^^(i)-{p$)+Р(\))-p(i,h)-ipU)-p(i-j+\,h}^. (13.52)

Для несоставных времен ожидания можно выразить распределение времени ожидания с помощью комбинации составных времен ожидания.

Если мы примем h = 1, то (13.50) может быть биноминальным разло­жением, записанным с помощью степени х , где t=74 х; Т— целое число, 0<т <1.

p{W< T+T}=e^y"Y,^<£^-P{W< T-j}, (13.53)

j=о J^!

гдep{W< T-j) определяется в (13.51).

Очень точная числовая оценка может быть получена при использова­нии (13.51), (13.52) и (13.53).