2. Алгоритм свертки для систем с потерями

Теперь рассмотрим группу пучков каналов с общим количеством и гомогенных пучков каналов. Гомогенными мы в данном случае называем каналы, имеющие одну и ту же скорость. На группу пучков каналов посту­пают N различных типов вызовов, называемых потоками, или классами. Вызов типа / требует d. пучков каналов (каналы, слоты) в течение всего времени обслуживания, то есть занятия и освобождения одновременно всех каналов d..

Процессы поступления вызовов — общие зависимые от состояния Пуассоновские процессы. Для /'-го процесса поступления вызовов интен­сивность прибытия в состоянии х. х d., то есть когда вызовы х. типа i обслуживаются, интенсивность равна (х). Мы можем ограничить число х. одновременных вызовов типа i так, чтобы:

О < Xj • dj < я, < п.

Будет естественно потребовать, чтобы я. было составным числом, кратным d_i. Эта модель описывает, например, систему, показанную на рис. 10.5.

Местная станция

Рисунок 10.5. Обобщение классического телетрафика показывает нагрузку ВРР и мультислотовый трафик. Параметры Х,₍ и Z описыва­ют нагрузку ВРР, тогда как d. обозначает число требуемых слотов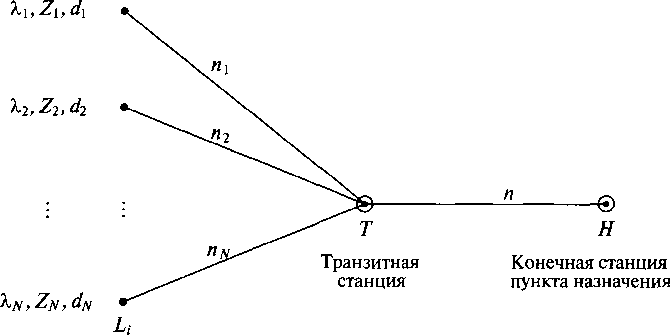

Упомянутая выше система может быть оценена эффективным спо­собом - алгоритмом свертки, впервые введенным в (Iversen, 1987 [40]). Сначала опишем алгоритм, а затем объясним на примере дальнейшие детали. Алгоритм свертки близко связан с формой произведения.

1. Алгоритм

Алгоритм представлен следующими тремя шагами.

Шаг 1. Вычислите вероятности состояния каждого потока нагрузки, как будто он является единственным в системе, то есть мы рассматриваем классические системы с потерями, как это отображается в лекциях 7 и 8. Для нагрузки потока / мы находим:

(10.22)

Важны только условные значения р. {х), так что мы можем выбрать q. (0) = 1 и вычислить значения q. (х) относительно д. (0). Если элемент д. (л:) становится больше, чем К (например 10¹⁰), тогда мы можем разделить все значения g. (j); 0 <j < х, на К. Чтобы избежать любых проблем вычислений, в дальнейшем желательно нормировать условные вероятности состояний так, чтобы:

Шаг 2. Последовательным свертыванием (оператор свертывания *) мы вычисляем совокупную вероятность состояния для полной системы за исключением потока нагрузки /:

(10.23)

0м ⁼ il *il *"'* ^pj-1 * Ри± Pn-

Сначала свертываем P_{ и Р_г и получаем Р_[2, который свертывается с Р_у и т.д. Оба закона — коммутативный и ассоциативный — справедливы для оператора свертывания и определены обычным способом (секция 3.2):

Заметьте, что производится усечение пространства состояний к п состояниям. Даже если Р. и Р нормированы, результат свертки в общем случае не нормирован из-за усечения. Его рекомендуется нормировать после каждого свертывания, чтобы избежать любых проблем при вычис­лении в течение этого шага и на следующем.

Шаг 3. Вычислите потери по времени Е., потери по вызовам В. и поте­ри по нагрузке С потока Это может быть сделано в процессе свертки:

Qn = Qn/i * Pi •

Свертка заканчивается:

QnU) = i,Q_NAj-x) •pi(x) = £pl0), (10.26)

х=0 x=0

где для p‘_x(j)i обозначает поток нагрузки, j — общее количество занятых каналов их - число каналов, занятых потоком /. Шаги 2-3 повторяются для каждого потока нагрузки.

Далее мы получаем формулы для Е., В. и С..

Потери по времени Е. для нагрузки потока i получаются:

Ei^YjMVQ- (10.27)

jeS_Ei

где

S_Ei = {(x,j)\x<j < пл(х>п i- di) v (/ > n - di)} ,

Суммирование по всем S_£l расширенным состояниям, где вызовы, принадлежащие классу блокированы: набор (х > п. - d) соответству­ет состоянию, в котором поток нагрузки / использовал свою квоту, и 0’ > п - d.) соответственно число состояний с меньшим чем d_t свободных каналов. Q — нормировочная константа:

Q^UQnH).

j=0

(На этом этапе мы обычно нормируем вероятности состояния так, чтобы Q= 1).

2? — потери по вызовам для нагрузки потока / — это отношение числа блокированных попыток вызова к общему числу попыток вызовов (оба числа берутся для потока нагрузки / в единицу времени). Мы находим:

'Ilh(x)-Pⁱ_x(j)

В ^Е‘

Ъ = VV ' (Ю.28)

2 21ь(х)-р‘_х0)

j=О *=0

Потери по нагрузке С. Мы определяем их, как обычно предложен­ную нагрузку, которую обслуживает бесконечная группа пучков каналов. Обслуженная нагрузка для нагрузки потока /:

Ъ = Цх-рЩ). (10.29)

у'—0 х=0

Таким образом, мы находим:

^ _ Л/" Я ^с‘⁼~аГ-

Алгоритм реализован в программном обеспечении ATMOS (Листов, Сааби, Иверсен (Listov, Saabye и Iversen, 1989 [74]). Требование к памяти (накопителю) пропорционально я. Она используется для вычисления веро­ятности состояния потока нагрузки, когда это необходимо. Практически мы используем память, пропорциональную п х N, потому что сохраняем промежуточные результаты свертывания для более позднего повторного использования. Можно показать (Иверсен и Степанов, 1997 [42]), что нам необходимо (4 х Л"- 6) свертывания, когда мы вычисляем характеристики нагрузки для всех N потоков нагрузки. Таким образом, время вычисления подчиняется линейной зависимости от Л" и квадратичной для п.

Пример 10.4.1: развертка

В принципе мы можем получить Q^. из Q_N разверткой и затем в течение повторной свертки Р. вычислить критерии качества работы. При этом способе мы не должны повторять все свертки (10.23) для каждого потока нагрузки. Но при осуществлении этого подхода имеются проблемы вычислений. Свертка, с точки зрения вычисления, очень устойчива, а развертка вычисляется не всегда. Однако мы можем применить развертку в некоторых случаях, напри­мер, когда источники нагрузки имеют два состояния - вкл\выкл.