3. Мультислотовая нагрузка

В системах с интеграцией служб требуемая пропускная способность может зависеть от типа обслуживания. Например, для обслуживания телефонного соединения с передачей только речи требуется один канал (слот), тогда как, например, для передачи видеоизображения может потребоваться d каналов одновременно. Мы получаем дополнительные ограничения:

(10.19)

О < dj-ij < rij < п, j =1,2,..., N,

N

и

(10.20)

где / — фактическое число вызовов типа j. Результирующая диаграмма переходов состояний будет обратима, и будет иметь форму произведения.

Ограничения соответствуют, например, физической модели, пока­занной в рис. 10.5.

Предложенная нагрузка А обычно определяется как среднее число попыток вызова на среднее время пребывания в системе. Если мы изме­

ряем обслуженную нагрузку Y. как среднее число занятых каналов, то потерянная нагрузка, измеренная в каналах, получается:

A_e=f_JAjdj-f_JYj. (10.21)

М J=1

Таблица 10.1. Два потока нагрузки: Пуассоновский процесс (при­мер 7.5.1) и биноминальный процесс (пример 8.5.1) - поступает на один и тот же пучок каналов

Поток 1: Нагрузка PCT-I	Поток 2: Нагрузка PCT-II
=2 вызова/единица времени (J.1 = 1 (единица времени “ *) Z\ = 1 (пиковость) d\ = 1 канал/вызов А \ - A-i/jj. 1 = 2 Эрл. и 1=6= и	Si = 4 источника у 2 = 1/3 вызова / в единицу времени / свободный источник /<2-1 (единица времени " *) Рг - У2/Ц2 = 1/3 Эрл./свободный источник Z2 = 1/(1 + Рг) = 3/4 (пиковость) di = 2 канал/вызов А2 = S2- Р2/(1 + Р2) = 1 Эрл. «2 = 6= П

Пример 10.3.1: Модель Роннблома (Ronnblom's model)

Первый пример модели мультислотового трафика был опублико­ван Роннбломом (1958 [92]). Статья рассматривает внешнюю нагрузку (исходящую и входящую) и внутреннюю нагрузку в учрежденческой теле­фонной станции (РАВХ) с двусторонними каналами. Внешняя нагрузка занимает только один канал на вызов. Внутренняя нагрузка занимает и исходящий канал, и входящий канал и таким образом требует двух кана­лов одновременно. Роннблом показал, что эта модель имеет форму про­изведения.

Пример 10.3.2: Два потока нагрузки

Проиллюстрируем вышеупомянутые модели маленьким исследова­нием. Мы рассматриваем пучок из 6 каналов, на который поступают два потока нагрузки, указанные в таблице 10.1. Пусть второй поток нагруз­ки — поток мультислотового трафика. Пусть в нашей системе может быть не более трех вызовов типа 2.

Мы должны определить только предложенную нагрузку, не опреде­ляя абсолютные значения интенсивности поступления и скорости обслу­живания. Предложенная нагрузка, как обычно, определяется как нагруз­ка, которую несет пучок из бесконечного числа каналов.

На рис. 10.4 показана двухмерная диаграмма переходов состояний. Полная сумма всех вероятностей состояний равняется 20,1704. После нормализации мы находим р(0, 0) = 0,0496 а также следующие вероятно­сти состояния и безусловные вероятности состоянийp(i, •) пр( •,/).

PCT-II

4_

27

► PCT-I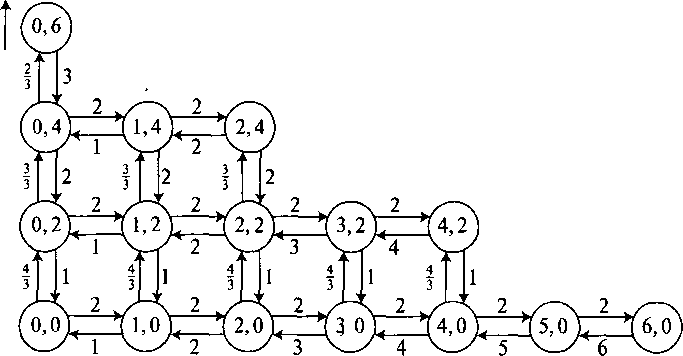

тогда, используя локальное равновесие вероятностей состояний, мы сможем найти условное состояние q(i,j), показанное ниже

p(*J)	i=0	i=l	i = 2	/ = 3	i = 4	i = 5	/ = 6
У =6	0.0073							0.0073
;=4	0.0331	0.0661	0.0661					0.1653
j =2	0.0661	0.1322	0.1322	0.0881	0.0441			0.4627
7=0	0.0496	0.0992	0.0992	0.0661	0.0331	0.0132	0.0044	0.3647
P(i, )	0.1561	0.2975	0.2975	0.1542	0.0771	0.0132	0.0044	1.0000

Глобальные вероятности состояния получаются:

р(0)=р(0,0) = 0.0496

/»(!)= /»(1,0) = 0.0992

р(2) = р(0,2) + р(2,0) = 0.1653

рО)= Р( 1,2)+ р(3,0) = 0.1983

р(4) = р(0,4) + р(2,2) + р(4,0) = 0.1983

/>(5) =/>(1,4)+ />(3,2)+ />(5,0) = 0.1675

р(6) = р(0,6) + р(2,4) + р(4,2) + р(6,0) = 0.1219

Критерии качества работы для потока 1

В соответствии со свойствами потока PASTA потери по времени (Е_х), потери по вызовам (В_х) и по нагрузке (С,) - равны. Мы найдем потери по времени Е_х:

Е! = р(6,0) + /?(4,2) + р(2,4) + рф, 6) = р{6),

Е_х = В_х = Ci = 0.1219,

Yi = 1.7562.

Критерии качества работы для потока 2

Потери по времени Е₂ (соотношение времени блокировки системы для потока 2):

Е₂ = р( 0,6) + р( 1,4) + р( 2,4) + р( 3,2) + />(4,2) + /7(5,0) + р( 6,0)

= />(5) + р(6),

Е_г = 0.2894.

Потери по вызовам В₂ (соотношение попыток вызова, блокирован­ных для потока 2):

Общее количество попыток вызова в единицу времени получено из безусловного (одномерного) распределения:

X/ = % • 0.3647 + • 0.4627 + \ • 0.1653 + • 0.0073 = 1.0616.

3 3 3 3

Число блокированных попыток вызова в единицу времени получа­ется:

xt = j- {p(5,0)+p(6,0)j +1 ■ {р(3,2)+р(4,2)}+1 • {р(1,4)+р(2,4)}+~ •р(0,6)

= 0.2462.

Следовательно,

В₂ = — = 0.2320.

•X/

Потери по нагрузке С₂ (соотношение блокированной и предложенной нагрузки):

Обслуженная нагрузка, измеренная для канала, получена из безуслов­ного (одномерного) распределения:

Yi =

j=о

Y₂ = 2 • 0.4627 + 4-0.1653 + 6 • 0.0073,

Y₂ = 1.6306 Эрл.

Предложенная нагрузка, измеренная на канал, равна d₂xA₂ - 2 Эрл. (таблица. 10.1). Следовательно, мы имеем:

2- 1.6306 С₂ = = 0.1848.

Рассмотренный выше пример имеет только 2 потока и 6 каналов, и общее количество состояний равняется 16 (рис. 10.4). Когда число потоков нагрузки и каналов увеличивается, число состояний очень быстро увеличи­вается, и невозможно оценить систему, вычисляя отдельные вероятности состояния. В следующей секции мы вводим алгоритм свертки для систем с потерями, который устраняет эту проблему увеличения состояний.