Лекция 12 Системы с ожиданием

нию, т.е. к левой стороне в начале интервала (текущее событие). Далее нас интересуют, главным образом, средние величины и характеристики, которые справедливы для всех дисциплин организации очереди, не нару­шающих нормальную работу (секция 13.4.2).

Терминалы Система очередей

Рисунок 12.5. Модель восстановления машин Пальма. Компьютерная система с S терминалами (диалоговая система) соответствует систе­ме с ожиданием и с ограниченным числом источников (см. случай Энгсета для систем с потерями)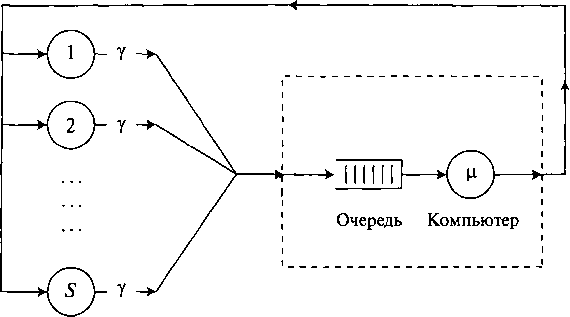

Состояние терминала

ч Время обращения >■;

Обслуживание

Ожидание -

Т,

T_w

Время

Рисунок 12.6. Отдельный терминал может быть в трех различных состояниях. Любой пользователь может работать активно на терми­нале (или думать), или он ждет ответа от компьютера. Последний временной интервал (время реакции) разделен на две фазы: фаза ожидания и фаза обслуживания

Абонент думает или работает

1. Вероятности состояния одного обслуживающего прибора

Рассмотрим теперь систему с S терминалами, которые связаны с одним компьютером. Предполагается, что времена размышления або­нента для каждого терминала экспоненциально распределены с интен­сивностью у = 1//и₍ и время обслуживания (выполнение компьютером работы) распределено экспоненциально с интенсивностью д = 1 /т_$. Когда есть очередь в компьютере, терминалы должны ждать обслуживания. Обслуживаемые терминалы или ждущие в очереди имеют нулевую интен­сивность поступления.

Состояние [/] определено как состояние, где в системе организации очереди (рис. 12.5) есть / терминалов, то есть компьютер либо свободен (/' = 0), либо работает (/ > 0), и (i-1) терминалов ждут все время, пока (г> 0).

Система организации очереди может быть смоделирована процессом «гибели и размножения» и диаграммой перехода состояний, показанной на рис. 12.7. Существует статистическое равновесие (эргодическая систе­ма). Интенсивности поступления заявок уменьшается, по мере того как длина очереди увеличивается, и интенсивность становится нулевой, когда все терминалы стоят в очереди.

Устойчивые вероятности состояния могут быть найдены, по рис. 12.7, с помощью уравнения сечения и выражены с помощью числа состояний S:

(12.35)

Согласно дополнительным ограничением нормировки, подставляя в = М/у, находим сумму всех вероятностей, которая равна:

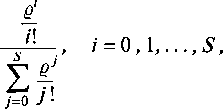p(S-i) = ^p(S)

(12.36)

(12.37)

/>(0) = E_x,s (в) •

Это — усеченное Пуассоновское распределение (7.9).

Мы можем интерпретировать систему следующим образом. Группе с S пучками каналов (терминалами) поступают вызовы от компьютера с экспо­ненциально распределенными интервалами поступления (интенсивность) |i.

Sy (S- 1)у (S- 2) у 2у у

Рисунок 12.7. Диаграмма переходов для системы организации очере­ди, показанной в 12.5. Состояние [ i ] обозначает число терминалов, которые либо обслуживаются, либо ожидают обслуживания, то есть S- / обозначает число терминалов, где пользователь либо размышля­ет, либо работает непосредственно с компьютером

Когда все S пучков каналов заняты (пауза на размышление или ввод), ком­пьютер свободен, и интенсивность поступления нулевая, но мы могли бы предположить, что все пучки еще генерируют вызовы с интенсивностью ц, которые потеряны в этой или другой группе пучков каналов (экспо­ненциальное распределение не имеет памяти). Компьютер, таким образом, предлагает нагрузку д = Ц/у S пучкам каналов, и мы имеем формулу (12.37). В-формула Эрланга справедлива для произвольных времен пребывания в системе (секция 7.3.3), и поэтому можно утверждать, что:

Теорема 12.1. Вероятности состояния модели восстановления машин

36. и (12.37) с одним компьютером и S терминалами справедливы в течение произвольных времен пауз (размышления и работа с компьютером), когда времена обслуживания компьютером являются экспоненциально рас­пределенными.

Отношение в - й/у^{: эт0} отношение среднего времени, когда пользо­ватель терминала думает 1/у, и среднего времени, когда компьютер обслу­живает терминал 1/ц. Это отношение называется сервисным отношением. В В-формуле Эрланга сервисное отношение соответствует предложенной нагрузке. Вероятности состояния определяются числом терминалов S и сервисного отношения. Вычисление по формулам (12.36) и (12.37) прово­дится, как и в В-формуле (7.29) Эрланга.