Курс Разработка телетрафика и планирование сетей

/ц (/ + 1) ц n\i яц п ц

Рисунок 12.1. Диаграмма переходов состояний М/М/п системы с ожиданием, имеющей п серверов и неограниченное число мест ожидания

2ц

Нас интересуют вероятности устойчивых состояний системы. В сек­ции 7.4 дана диаграмма переходов между состояниями (рис. 12.1). Принимая, что диаграмма находится в статистическом равновесии, получаем:

Х-р( 0) = ц-/>( 1),

Я. •/>(!) = 2 ц ./>(2),

X-p(i) = (/+1) ц-pO'+l) >

(12.1)

Х-р(п- 1) = п ц-р{п), Х-р(п) = «ц 'р(п+1) ,

Если А = V|a, ~ ^это предложенная нагрузка, то мы имеем:

X'p(n+j) = nvp(n+j +1) .

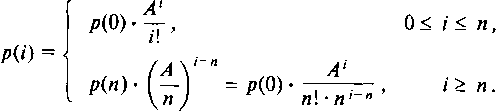
(12.2)

С помощью нормировки вероятностей состояний получаем:

Внутренние фигурные скобки содержат геометрическую прогрессию с коэффициентом прогрессии А/п. Условие нормализации может быть выполнено только для:

А<п (12.3)

Статистическое равновесие получено лишь для А < п. Иначе очередь будет увеличиваться до бесконечности.

Мы получаем значение р_п:

р(0)= — , А<п. (12.4)

У di ^ ^п /! ⁺ и! п - А

Уравнения (12.2) и (12.4) показывают вероятности устойчивых состояний.

1. Характеристики нагрузки систем с ожиданием

Для оценки производительности и рабочих характеристик системы нужно рассмотреть несколько характеристик. Они отражают вероятности устойчивых состояний.

1. С-формула Эрланга

Когда Пуассоновский поток вызовов не зависит от состояния систе­мы, вероятность того, что произвольный вызов должен будет ждать обслуживания в очереди, равна пропорции времени, когда заняты все обслуживающие приборы (свойство PASTA). Время ожидания - случай­ная величина, которая обозначается W. Для произвольного поступления вызовов имеем:

А^п п

= А А’ п ■ ^Л*"- <¹¹⁶>

⁺ 1 ⁺ 2! ^{+ +} (п - 1)! ⁺ и! п - А

Эта вероятность ожидания зависит только от А, т.е.произведения X и s. Формула имеет несколько названий: С-формула Эрланга, вторая формула Эрланга или формула Эрланга для систем с ожиданием. Она имеет различные обозначения в литературе:

E_Xn{A)=D=D_n{A)=p{W> 0}.

Клиенты либо обслуживаются немедленно, либо помешаются в оче­редь. Вероятность, что клиент обслуживается немедленно, равна:

£„= 1 -E₂JA).

Обслуженная нагрузка Уравняется предложенной нагрузке Л, так как ни одному вызову не отказывается в обслуживании, а процесс поступле­ния вызовов — Пуассоновский процесс:

п

00

• 

  1=1

  *=rt+l

  со

  

  п

  (12.7)

  = £г>(0+Х np(i)

Здесь применено уравнение равновесия.

Длина очереди — случайная величина L. Вероятность наличия клиен­тов в очереди в случайной точке времени:

А

p{L> 0} = y~jp{n)= ^ Е₂,„{А).

(12.8)

Здесь использовалось (12.5).

2. Числовая оценка

А < п.

Формула подобна В-формуле (7.10) Эрланга, за исключением коэф­фициента п/(п-А) в последнем элементе. Поскольку существует очень точная рекурсивная формула для числовой оценки В-формулы Эрланга (7.29), можно использовать следующие отношения для того, чтобы полу­чить числовые значения для С-формулы:

\-А {1- Е_к„(А)}/п ’

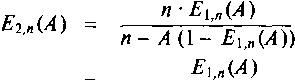
(12.9)

где элемент А{ 1 - Е_{х п} (А)}/п — средняя обслуженная нагрузка на канал в соответствующей системе с потерями. Для А > п мы имеем Е_{г п} (А) = 1. Это — вероятность того, что все клиенты поставлены на ожидание. С-формула Эрланга может быть выражена В-формулой:

(12.10)

(12.11)

1 1 1

Е₂,_п{Л) ~ E_U{A) E_X'„-i(A) ’

h,n(A) = h,n(A) ~ h,n-\(A),

где I - инверсия вероятности (7.30).

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Предложенная нагрузка

Рисунок 12.2. С-формула Эрланга для системы с ожиданием М/М/п. Вероятность Е₂ (А) для положительного времени ожидания показана как функция предложенной нагрузки для различных значений числа обслуживающих приборов п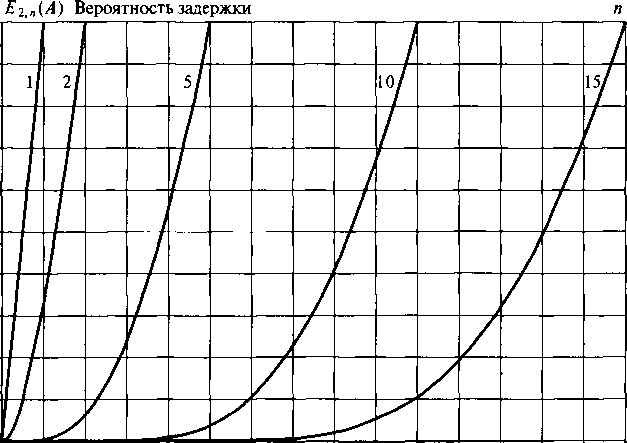

С-формула Эрланга была сведена в таблицу в Принципе Mo (Jensen, 1950 [50]) и показана на рис. 12.2.

1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3

0.2 0.1

0.0

3. Средняя длина очереди

Мы должны отличать длину очереди в произвольный момент време­ни и длину очереди, когда есть клиенты, стоящие в очереди.

Средняя длина очереди в произвольный момент времени

Длина очереди L в произвольной момент времени называется вир­туальной длиной очереди. Для произвольного клиента длина очереди определяется как свойство PASTA, т.е. Пуассоновский поток вызовов (математическое ожидание по времени = математическое ожидание по вызовам). Мы получаем среднюю длину очереди:

L_n = Е {L} в произвольный момент времени:

П

i=0 г'=я + 1

Поскольку А/п < с <1, ряд является равномерно сходящимся, опера­тор дифференцирования может быть вынесен за сумму:

{1 -(А/п)}²

А/п

(12.12)

Ь_п = Е₂,„(А)'~- п-А

Средняя длина очереди может интерпретироваться как нагрузка, которую обслуживают места ожидания очереди, и поэтому она иногда называется нагрузкой времени ожидания.

Средняя длина очереди, со временем ожидания больше нуля

Математическое ожидание времени и в этом случае равно математи­ческому ожиданию вызова. Условная средняя длина очереди будет:

Л (i-n)p(i)

i=n +1

nq

/=л+1

A/n

I pH)

i=

Pin)

(1 - A/n У

Pin) ~r ■

n-A

ⁿ (12.13)

n-A

Применяя (12.8) и (12.12), получаем:

L

^Lnq=J{L^}’

где L — случайная переменная, обозначающая длину очереди.