Л1

п\

(7.10)

А^п + —-

Е„(А)=р(п) =

Это - известная В-формула Эрланга (1917, [11]). Она обозначается £ (А) = Е_{х п} (А), где указатель «1» рассматривается как указатель названия первая формула Эрланга.

Потери по вызовам

v=0

Вероятность, что случайный вызов будет потерян, равна отношению всех попыток вызовов к числу блокированных попыток вызова. Если мы рассматриваем единицу времени, то находим В = В_п(А):

(7.11)

Обслуженная нагрузка

Если мы используем усеченное уравнение между состоянием [г-1], и [/'], то получим:

п п

(7.12)

<=1 ;=] I^м

• = А-{1-Е„(А)},

где А — предложенная нагрузка. Обслуженная нагрузка будет меньше и чем А, и чем п.

Потери по нагрузке

А_е = А - Y= А • Е_п(А).

А — Y С = —— = Е_п(А).

Мы, таким образом, имеем Е=В=С, потому что интенсивность вызова не зависит от состояния. Это свойство — PASTA (Poisson Arrivals See Time Averages — Пуассоновское поступление вызовов, наблюдаемое за среднее время) — справедливо для всех систем с Пуассоновскими потока­ми вызовов. Во всех других вариантах, по крайней мере, два из трех случа-

ев потерь различны. В-формула Эрланга показана графически на рис. 7.3 для некоторых выбранных значений параметров.

Нагрузка, которую обслуживает I-ый канал (использование а..)

1. Вероятность блокировки Еп(а)

   

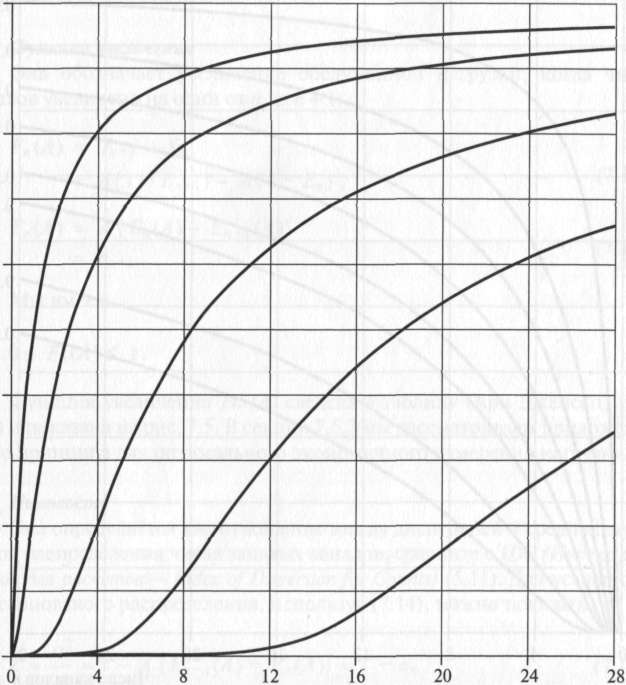
   Предложенная нагрузка л

   Рисунок 7.3. Вероятность блокировки Е_п(А) как функция предложен­ной нагрузки для различных значений числа каналов — п (7.9)

   1.0

   Случайный поиск. В этом случае все каналы в среднем обслуживают одну и ту же нагрузку. Полная обслуженная нагрузка не зависит от стратегии поиска, и мы можем найти использование:

Эта функция показана на рис. 7.4, и мы наблюдаем, что в данном случае при потерях Е получается самое высокое использование для боль­ших групп канала (экономия из-за масштаба).

Использование а Е

Число каналов п

Рисунок 7.4. Среднее удельное использование а (7.13) как функция числа каналов п для заданных значений потерь Е

2. Обусловленный поиск — последовательный поиск: нагрузка, которую обслуживает канал, есть разность между нагрузкой, потерянной /-1 каналами, и нагрузкой, потерянной / каналами:

(7.14)

Отметим, что нагрузка, которую обслуживает канал /, не зависит от общего числа каналов. Таким образом, каналы после /-го канала не влияют на нагрузку, обслуживаемую каналом /, т.е. между каналами нет никакой обратной связи.

Функция увеличения

Она обозначает увеличение обслуженной нагрузки, когда число каналов увеличено на один от п до п + 1:

(7.15)

F„(A) = Y_n+1- Y„,

= A{\-E_n+X}- A{\-E_n),

(7.16)

F_n{A) = A {E„{A) - E„+\ (/4)}

*- &П+1 •

Мы имеем

0< F„G4)< 1.

Функция увеличения Fn (А) сведена в таблицу (Арн Дженсен, 1950 [50]) и показана на рис. 7.5. В секции 7.6.2 мы рассматриваем приложение этого принципа для оптимального экономичного измерения нагрузки.

Пиковость

Она определяется как отношение между дисперсией и средней вели­чиной распределения числа занятых каналов, сравните с IDC (Индекс рас­сеяния для расчетов — Index of Dispersion for Counts) (5.11). Для усеченного Пуассоновского распределения, используя (7.14), можно показать

(7.17)

Размерность [число каналов]

В группе с обусловленным поиском мы можем таким образом оце­нить пиковость нагрузки, которую обслуживает последний канал.

Число каналов п

Рисунок 7.5. Функция увеличения F_n (А) (7.16) по В формуле Эрланга. F_n{A) при последовательном поиске равна нагрузке а_я+1, при увеличе­нии числа канала (п+ 1)

Продолжительность состояния [i]

Полная интенсивность для перехода из состояния [г] постоянна и равна (к + г'р), и поэтому продолжительность времени в состоянии [г] (время пребывания) экспоненциально распределена с функцией плотности:

/ДО = (Я + г>) • е^- ‘, Q<i<n,

-г и <^7Л8>

fn(t) = (rtfi)'Q ^(п>4)‘ , i= п.

1. Общая процедура для диаграмм перехода состояний

Самый важный инструмент в теории телетрафика — формулировка и решение задач с помощью моделей, посредством применения диаграмм перехода состояния. Из предыдущих секций мы можем установить сле­дующую стандартную процедуру для того, чтобы применить диаграмму перехода состояния. Она состоит из множества шагов и может быть сфор­мулирована в общих терминах. Эта процедура также применима для мно­гомерных диаграмм перехода состояния, которые мы рассмотрим позже. Процедура всегда проходит следующие шаги.

а. Созданием диаграммы перехода состояния:

• определяют состояния системы,

• рисуют состояния как окружности,

• рассматривают состояния по одному и вводят в рисунок все возможные стрелки переходов от одного состояния к другому. При этом учитывают следующие процессы:

• процесс поступления вызовов (вновь прибывшая заявка или сдвиг фаз в процессе поступления вызовов),

• процесс окончания (время окончания обслуживания или сдвиг фазы).

Этим способом мы получаем законченную диаграмму перехода состояния.

б. Составить уравнения, описывающие систему.

Если условия для статистического равновесия выполнены, уравне­ния устойчивости состояний могут быть получены из:

• уравнений узла,

• уравнения сечения.

в. Решить уравнения равновесия, отображающие статистическое рав­новесие.

• выражают все вероятности состояния, например, с помощью вероятности нулевого состояния [0] —р (0),

• нормализацией находят р (0).

г. Вычислить критерии качества работы, выраженные вероятностями состояния.

На практике мы находим ненормализованное значение вероятности состояния #(0), равное единице, а затем вычисляем относительную вели­чину q(i), (/' = 1, 2....). Нормализуя ее, находим:

где

я

(7.20)

Qn = Z 0(^v> •

v=0

Тогда потери по времени получаются равными:

(7.21)