1. Мультиноминальное распределение

Для более поздних приложений важны следующие свойства. Если мы полагаем, что точка выбрана наугад в пределах временного интер­вала, подчиняющегося распределению Кокса, то вероятность, что эта точка — в пределах фазы i, равна:

—, /=1,2,...Д. (4.36)

т

Если мы повторяем этот эксперименту раз (независимо), то вероят­ность, что фаза / наступала у. раз, определяется с помощью мультиноми- нального распределения (оно же - полиномиальное распределение):

р{у\уьу2,-,у_к) = ( ^У (4.37)

Vji У2 • • • У к) V гп > \ т J \ т )

где

у= £л,

;=1

и

(4.38)

У-

1У2 ... Ук) У\'-'У2- Ук'-

Элементы в (4.38) называются мультиноминальными коэффици­ентами. Благодаря свойству экспоненциальных распределений — отсут­ствию памяти, — мы имеем полную информацию об остаточном времени «жизни», если знаем номер текущей фазы.

2. Принципы декомпозиции

Диаграммы состояния — полезный инструмент для того, чтобы анали­зировать Распределения Кокса. Ниже приводится фундаментальная харак­теристика экспоненциального распределения (Iversen и Nielsen, 1985 [41]).

Теорема 4.1. Экспоненциальное распределение с интенсивностью X может быть представлено как два фазовых распределения Кокса, где пер­вая фаза имеет интенсивность и вторая — фазовую интенсивность X (сравните с рис. 4.8).

ЛОР.

Согласно Теореме 4.1 гиперэкспоненциальное распределение с ' / фазами эквивалентно распределению Кокса с тем же самым числом фаз. Случай / = 2 показан на рис. 4.10.

Другое свойство распределений Кокса ([versen и Nielsen, 1985 [41]):

Теорема 4.2. Фазы в любом Распределении Кокса можно упорядочить как Х>Х₊₁.

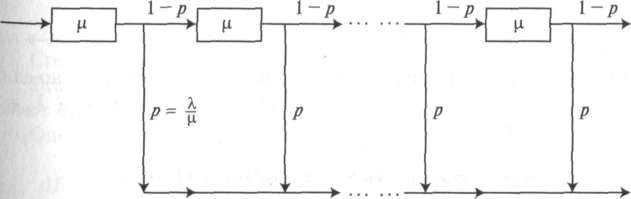
Теорема 4.1 показывает, что экспоненциальное распределение экви­валентно гомогенному распределению Кокса (здесь «гомогенное» означа­ет «имеет одну и ту же интенсивность во всех фазах») с интенсивностью т и бесконечное число фаз (рис. 4.8). Заметим, что переходные вероятности постоянны.

Рис. 4.9 показывает взвешенную сумму к распределений Эрланга, где весовые коэффициенты распределены геометрически.

Рисунок 4.8. Экспоненциальное распределение с коэффициентом Я эквивалентно показанному распределению Кокса (теорема 4.1)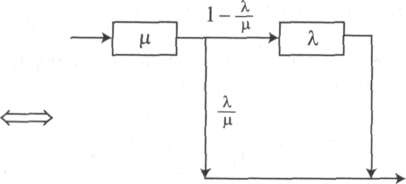

Рисунок 4.9. Экспоненциальное распределение с коэффициентом X может быть декомпозировано с помощью последовательного раз­ложения в составное распределение гомогенных к распределений Эрланга с коэффициентом , где весовые коэффициенты геоме­трически распределены (частное р = Vji)-