1. Гиперэкспоненциальное распределение

В этом случае ЩХ) - дискретно. Предположим, что нам даны сле­дующие значения:

Х\, Х₂, . . . , Хк , и что ЩХ) имеет положительные и увеличивающие значения: Рь Рг, ■■■ , Рк,

где

к

(4.23)

Y,Pi=i •

i=i

Для всех других значений ЩХ) является постоянным. В этом случае (4.20) становится: _к

F(t)= 1- Y_Jp_i-e~^h', t> 0. (4.24)

1=1

Средние величины и коэффициент формы могут быть найдены из (3.36) и (3.37) (а, = т_{= У\):

Л

Z

(4.25)

т

PI

\ * j=l ^А1

(4.26)

> 2.

1=1

<= = ² <£0

i=l

Если к = 1 или все X. равны, мы получаем экспоненциальное рас­пределение.

Распределения этого класса называются гиперэкспоненциальными распределениями, и могут быть получены комбинацией к параллельных экспоненциальных распределений, где вероятность выбора /'-го распре­деления — р.. Распределение называется плоским, потому что увеличения его функции распределения от 0 до 1 идет медленнее, чем при экспонен­циальном распределении.

Практически, трудно оценить больше, чем один или два параметра. Самый важный случай - для п = 2(p_t-р,р₂-\ -р)

F(t) = 1 - р • e~^Xl' - (1 - р) • еГ^Х2‘. (4.27)

Статистические проблемы возникают, даже когда мы имеем дело с тремя параметрами. Так, для практических приложений мы обычно выби­раем X. = 2Х • р. и, таким образом, уменьшаем число параметров до двух.

F(t) = 1 - pe~^2lpt - (1 - р)е~^ии-^р)‘. (4.28)

и коэффициент формы получаются равными:

Средняя величина

1

1_

2р(1- р) '

(4.29)

При таком выборе параметров две ветви имеют тот же самый вклад в среднюю величину. Рис. 4.5 иллюстрирует пример.

4. Распределения Кокса

Комбинируя крутые и плоские распределения, мы получаем общий класс распределений (распределения фазового типа), которые может быть описаны с помощью экспоненциальной фазы в последовательном и параллельном случае (например, к х I матрицу). Чтобы проанализиро-

вать модель с таким видом распределений, мы можем применить теорию Марковских процессов, для которых имеются мощные инструментальные средства, такие, как метод диаграмм состояний (фазовый метод). В общем случае мы можем учесть обратную связь между состояниями (фазами).

Число наблюдений

О 5 10 15 20 25

Time

Рисунок 4.5. Функция плотности (частотная) для времен пребывания в системе наблюдаемых линий на местной станции в течение часа наибольшей нагрузки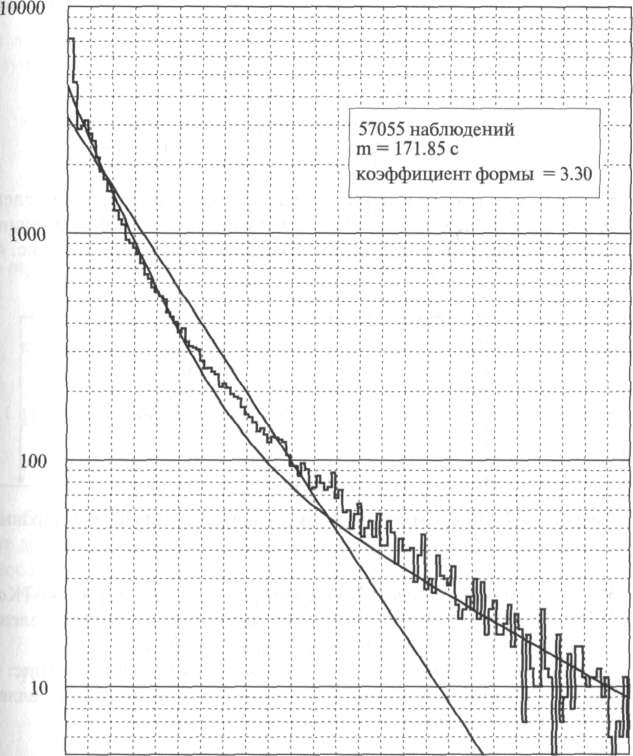

Рисунок 4.6. Распределение Кокса - обобщенное распределение Эрланга, имеющее параллельные и последовательные экспоненци­альные распределения. Диаграмма состояния эквивалентна рис. 4.7.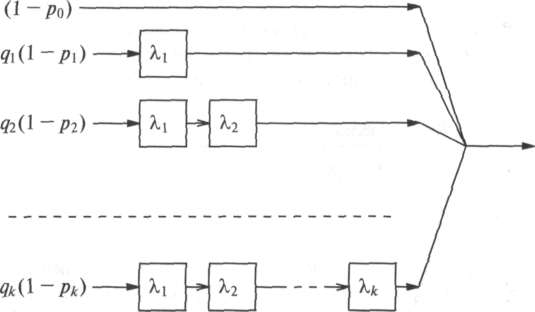

Рисунок 4.7. Диаграмма состояний распределения Кокса (сравните с рис. 4.6.)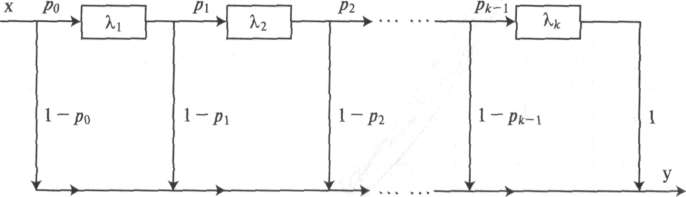

Рассмотрим распределение Кокса, которое показано на рис. 4.6 (Кокс, 1955 [17]). Оно также иногда называется распределением эрланговского разветвления (иначе, распределением Эрланга с ветвями).

Средняя величина и дисперсия этого распределения Кокса (рис. 4.7) получаются из формулы в секции 3.2 для последовательных и параллель­ных случайных переменных, как это показано на рис. 4.6:

»»i = XftO-л)(Лт"1 > (⁴-³°)

1=1 ( j=l Ч J

где

Qi = Ро -Pi -Pi Pi-i. (4.31)

Выражение q. (1 -р) — вероятность перехода процесса, когда он нахо­дится в /-ом состоянии. Средняя величина может быть выражена простой формулой:

(4.32)

т

i=l А/ /=1

где т_] . = — средняя величина в /-том состоянии. Второй момент случается

/с

4 {•«-*>■ ЙИШ-

де т₂. получен из (3.8): /я₂, = а², + т\ .; это можно записать как:

^<4'³⁴⁾

После чего получаем дисперсию (3.8):

о¹ = т₂ - т\.

Сложение двух распределений Кокса для случайных переменных ^_ает другое распределение Кокса для случайной переменной, то есть этот асс является замкнутым по отношению к сложению.

Функция распределения Кокса может быть записана как сумма экс- оненциальных функций:

(4.35)

к

1- F{t)=

i=i

к

0< YjCi< 1, 1=1

-00 < С i < + 00