1. Минимум к экспоненциально распределенных случайных переменных

Пусть две случайных переменные Х_г и ^являются взаимно незави­симыми и экспоненциально распределенными с интенсивностями А,, и Х₂, соответственно. Новая случайная переменная Xопределяется как:

X = min{X₁,Z₂} .

Функция распределения X равна:

р{Х< /}=1 -_е-<^х’^+х’>'. (4.6)

Эта функция распределения - тоже экспоненциальное распределе­ние с интенсивностью (1, + Я₂).

Согласно предположению, что первое (наименьшее) событие проис­ходит в пределах временного интервала t, t+dt, вероятность, что случай­ная переменная Х_х будет реализована первой (то есть, в этом интервале появится первой, а другая возникнет позже), будет равна:

P{t<X , < t + dt}- P{X₂>t} P{t<X < r + df>

р{Х₁<Х₂1 о =

A,i e ^k,t dt • e ^X2t (X,i+ A₂)e“<^x>⁺^>'df

Xi

—, (4.7)

1. ! + A, 2

то есть, независима от t. Таким образом, мы не должны интегрировать по всем значениям t.

Эти результаты могут быть обобщены на к переменных, и прини­маться как основной принцип методики моделирования, называемый метод рулетки или метод моделирования Монте-Карло.

2. Комбинация экспоненциальных распределений

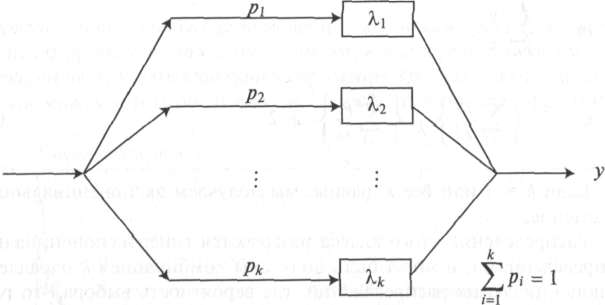
Если с помощью одного экспоненциального распределения (то есть одного параметра) мы не можем описать достаточно детально временные интервалы, то нам, вероятно, придется использовать комбинацию двух или больше экспоненциальных распределений. Пальма ввел два класса распределений: крутое и плоское. Крутое распределение соответствует набору последовательных, стохастических независимых экспоненциаль­ных распределений (рис. 4.2), а плоское соответствует параллельным экс­поненциальным распределениям (рис. 4.4). Такая структура естественно позволяет описать процессы нагрузки в телекоммуникации и сетях пере­дачи данных.

Комбинируя крутое и плоское распределения, мы можем получить произвольно хорошее приближение для любой функции распределения (см. рис. 4.7 и секцию 4.4). Диаграммы на рисунках 4.2 и 4.4 называются фазовыми диаграммами (или диаграммами состояний).

	А-1		Я,2		^к

Рисунок 4.2. Комбинируя к экспоненциальных распределений последовательно, получаем крутое распределение (е<2). Если все к распределения идентичны (А, = А), то мы получаем к распределение Эрланга

2. Крутые распределения

Крутые распределения также называют гиперэкспоненциальными распределениями или обобщенными распределениями Эрланга с коэф­фициентом формы в интервале 1<е<2. Эта обобщенная функция рас­пределения получена свертыванием к экспоненциальных распределений (рис. 4.2). Здесь мы рассматриваем только случай, где все к экспоненци­альных распределений идентичны. Тогда мы получаем следующую плот­ность функция, которая называется к распределением Эрланга (распределе­ние Эрланга k-го порядка):

/W* ^х>0’ * = 1,2,.... (4.8)

(К- I)!

00 ,

F(t) = X • e^-Xi (4.9)

j=k J'

к-\ .

= 1 - Z ” ’ (4.10)

;=о У'!

Следующие моменты могут быть найдены с использованием (3.31) и (3.32):

т - — , (4.11)

X

о² = 4т’ <⁴-¹²)

,

£ — 1 + —j ~ 1 ⁺ ~Г > (4.13)

т²- к

i-и нецентральный момент:

(/ + к- 1)! /IV — ' ^(4Л4) Функция плотности получена в секции 6.2.2. Средний остаток вре­мени «жизни» /и, _г(х) для х > 0 будет меньше, чем средняя величина:

т\'_Г(х) < т, х > 0.

Рисунок 4.3. к распределения Эрланга со средней величиной. Случай к = 1 соответствует экспоненциальному распределению (функции плотности)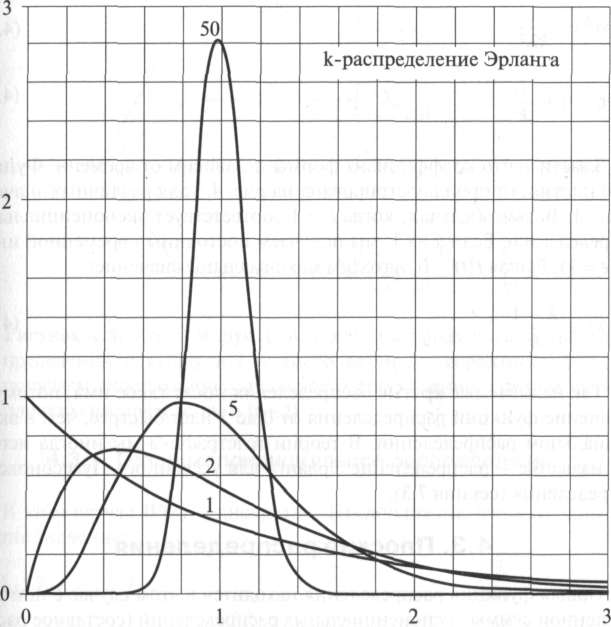

С этим распределением мы имеем два параметра (к, к), доступные для наблюдений. Средняя величина часто сохраняется фиксированной. Чтобы изучить влияние параметра к в функции распределения, мы нор­мализуем все к распределения Эрланга к одной и той же самой средней величине как 1, распределение Эрланга, то есть экспоненциальное рас­пределение заменим средним значением 1Д, a t - на kt или X на Хк:

(4.17)

2

кХ²

(4.18)

Заметим, что коэффициент формы независим от времени. Функция (4.15) плотности проиллюстрирована на рис. 4.3 для различных значений к с X = 1. Возьмем случай, когда к = 1 соответствует экспоненциальному распределению. Если к —> 1, мы получаем постоянный временной интер­вал (е = 1). Решая f(t) = 0, находим максимальное значение:

(4-19)

к

Так называемые крутые распределения носят такое имя, потому что увеличение функций распределения от 0 до 1 идет быстрее, чем в экспо­ненциальном распределении. В теории телетрафика мы иногда исполь­зуем название — распределение Эрланга для усеченного Пуассоновского распределения (секция 7.3).

Общая функция распределения находится в этом случае с помощью взвешенной суммы экспоненциальных распределений (составное распре­деление) с коэффициентом формы е>2:

00

о

(4.20)

X > 0, t> О

Функция веса может быть дискретна или непрерывна (интеграл Стилтьеса). Этот класс распределения соответствует параллельной ком­бинации экспоненциальных распределений (рис. 4.4). Функция плот­ности называется полностью монотонной с чередующимися знаками (Пальма, 1957 [82]):

(4.21)

(_1)V ./(v)_W> 0.

Среднее остаточное время «жизни» m_{x г} (х) для всего х > О является большим, чем средняя величина:

(4.22)

m\_ir(x) > т, х > 0.

Рисунок 4.4. Комбинируя к экспоненциальных параллельных рас­пределений и выбирая /' — число ветви / с вероятностью р., мы получаем гиперэкспоненциальное распределение, которое является плоским распределением (е>2)