Пример 3.2.1: Биноминальное распределение и испытания Бернулли

Пусть вероятность успеха в испытании (например, бросание кубика при игре в кости) равна р, а вероятность отказа равняется I —р. Число успехов в единственном испытании тогда получается с помощью распре­деления Бернулли:

!:?: <^з-^з4>

Если мы проведем 5 испытаний, то биноминальное распределение числа успехов

Ps(i) = ^У(1-/»)^5-/ (3.35)

получается сборкой S распределений Бернулли. Если мы делаем одно дополнительное испытание, то распределение общего количества успехов получается сверткой биноминального распределения (3.35) и распределе­ния Бернулли (3.34):

Ps+i(i) = Ps(0'Pi(Q)+ Ps{i~ 1)-/M(1)

= (f) P¹ (!-/>)*“' *(!-/»)+ (..f ₁У"¹(¹"/»)^,"^Ж\Р

2. Параллельные случайные переменные

Взвешивание / независимых случайных переменных, где i-ая пере­менная появляется с весовым коэффициентом р., дает

е

1=1

а средняя величина /и, . и дисперсия of сумма случайных переменных имеет следующую среднюю величину и дисперсию:

е

m = YjPi'm_u> (3.36)

;'=1

ст² = £ pi • (ст?+ т\,)-т². (3.37)

(=1

В этом случае мы должны взвесить нецентральные моменты. Для j-го момента мы имеем:

£

= YjPi'^mU > (³-³⁸>

ы\

где т.. — j-ый нецентральный момент распределения i-го интервала.

F(t) = Zu Pi ’ Ft(t). (3.39)

i=i

Подобная формула справедлива для функции плотности:

f(t)= •/,(/).

/=1

Взвешенная сумма распределений называется составным распреде­лением.

2. Стохастическая сумма

Под стохастической суммой мы понимаем сумму стохастических слу­чайных переменных (Feller, 1950 [27]). Рассмотрим группу направлений без перегрузки, где процесс поступления вызовов и времена пребывания в системе стохастически независимы. Если мы рассматриваем фиксиро­ванный временной интервал Т, то число поступления заявок - случайная переменная N. Ниже переведены свойства числа N:

N: плотность p(i),

средняя величина m _{t п}, (3.40)

дисперсия а².

Число поступлений вызовов / имеет время пребывания в системе Ti. Все Ti имеют одно и то же распределение, и каждое поступление (запрос) прибавляет некоторое число единиц времени (времени пребывания в системе), которые являются случайными переменными со следующими характеристиками.

(3.41)

N: функция плотности/(/), средняя величина т_{ дисперсия а².

Весь объем нагрузки, который получен из-за поступления зая­вок (запросов), пребывающих в пределах рассматриваемого временного интервала Г, — случайная переменная:

N ■

(3.42)

Рисунок 3.3. Стохастическая сумма может интерпретироваться как комбинация последовательно/параллельных случайных переменных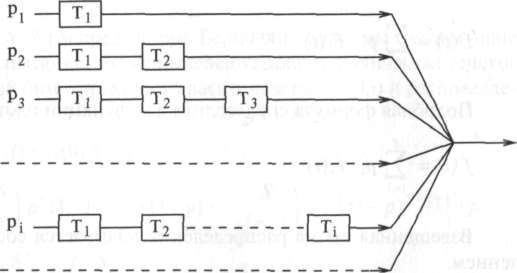

Далее мы принимаем, что Г и /V стохастически независимы. Это условие выполняется при условии нулевой перегрузки.

Следующие выводы правильны и для дискретных, и для непрерыв­ных случайных переменных (суммирование можно заменить интеграцией или наоборот). Стохастическая сумма становится последовательной и параллельной комбинацией случайных переменных, как показано на рис. 3.3. Для данной ветви / мы находим (рис. 3.3):

m\,i = i'm _ht>

(3.43)

(3.44)

2 • 2 of - I'of,

/=1

m₂,i = i • of + (i • m_u)². (3 45)

Суммируя по всем возможным значениям (ветвям) i, мы получаем:

оо

^т\ ,s= Y^P{i)'^mU

i=1

00^

i=1

^m\ ,s — (3.46)

W2,_S = J^P(0 • W

i=l

= ^P(0 *{ i-o? + (i-mi,t)²},

_ ^,=1 . 2 2

^2,1 w* • a_r + /n j, • ffl2,n » (3.47)

o² =«!,„• of + m\y (m₂,_n - m\_n),

2 222

a_s =/«,,„ -a, + -ct„ . _{(3 48)}

Можно отметить, что есть два элемента, составляющие полную дис­персию: один элемент отображает, что число вызовов — случайная пере­менная (о²), и второй — что продолжительность вызовов — случайная переменная (о,²).

Пример 3.3.1: Специальный случай 1: N = n = constant (т = п)

m\_iS = п • т \_tt,

о? = о?-и. (3.49)

Это соответствует числу вызовов поступющих в одно и то же время, при измерении объема трафика мы можем оценить среднее время Удержания.

Пример 3.3.2: Специальный случай 1:T = t = constant (т = t)

и» i,* = т !,„• f,

(3.50)

Если мы изменяем масштаб от 1 до т_{] ;}, то среднее значение есть произведение т_{х (}на дисперсию /и² ₍. При среднем числе вызовов т_{ = 1 расчет числа вызовов является проблемой.