Пример 3.1.2: Постоянный временной интервал

Для постоянного временного интервала продолжительностью И мы имеем:

/и,- = h‘.

1. Остаток времени «жизни»

Мы хотим найти распределение времени остатка «жизни», при усло­вии, что достигнут уже некоторый возраст х > 0. Условное распределение F(t + х|х) определено следующим образом, принимая р(Т> х) > 0 и

,17->,мг>*)= ^рНТ>!:г17^>х))

р{Т > х} p{T>t + х}

р{Т >х\

1- F(t+ х)

1- F(x)

И, таким образом:

F(t + xlx) = р{Т< t+ xl Т >х}

(3.11)

F(t+ х)- F(x)

1 - F(x) ’

^f(!+xM = Trm- ^<312)

Рис. 3.1 иллюстрирует эти вычисления графически.

Средняя величина /и, _г остаточного времени «жизни» может быть представлена как (3.4):

1. ⁰⁰

mi Ах) = YZJ(x) • J (I-^F(^t+x)} ^dt’ х>0. (3.13)

(=0

Показатель время «гибели» х, то есть вероятность, что рассматри­ваемое время «жизни» заканчивается в пределах интервала (х, x+dx),

при условии, что возраст х был достигнут, получается из (3.11), позволяя определить t = dx:

р,(х) • dx

/’(x + dx)- F(x) 1 - F(x)

(3.14)

1- Fix)

d F(x)

Рисунок 3.1. Функция плотности остаточного времени «жизни», обусловленной данным возрастом х (3.11). Пример основан на рас­пределении Вейбулла* We (2,5), где х = 3 и F(3) = 0,3023

Распределение Вейбулла (Weibull distribution) - распределение вероятностей непрерывной ^слУчайной величины X, функция распределения которой задается формулой

х>0 х< О

ш- /! (ff Л

I о,

Условная функция плотности F(x) также называется функцией интен­сивности отказов. Если приводится эта функция, то F(x) может быть полу­чена как решение следующего дифференциального уравнения:

^^+Ji(x)-f(x)=ii(x), (3.15)

j- J ц(и)<1и j ,

f(t)= [i(t) • exp j-J n(«)d«j .

F(t) = 1 - exp

которое имеет следующее решение (предполагая, что F(0) = 0):

(3.16)

(3.17)

Показатель «гибели» ц(?) является постоянным тогда и только тогда, когда время «жизни» имеет экспоненциальное распределение (часть 4).

Это фундаментальная характеристика показательного (экспоненци­ального) распределения, её называют Марковским свойством или свой­ством без последействия (при отсутствии памяти (возраста)): вероятность завершения не зависит от фактического возраста (истории) (секция 4.1).

Можно было бы ожидать, что среднее остаточное время «жизни» т_{] г} (х) уменьшится при увеличении х, поскольку ожидаемое остаточное время жизни уменьшается, когда возраст х увеличивается. Но это верно не для всех случаев. Для показательного распределения с коэффициентом формы е = 2 (секция 5.1) мы имеем /и, _г = т. Для распределений перевала

1. < е < 2 мы имеем /и, , = т. (секция . 4.2), тогда как для плоских распреде­лений 2 < е < верно /я, _г>т (секция. 4.3).

Пример 3.1.3: Распределение времени ожидания

Рассмотрим систему организации очереди с бесконечной очередью, где любой клиент не может быть заблокирован. Распределение времени ожидания W (t) для случайного клиента обычно имеет положительную вероятность при t = 0, потому что некоторые из клиентов обслуживаются немедленно без какой-либо задержки. Мы, таким образом, имеем W_s (0) > 0. Распределение времени ожидания W₊ (Г) для клиентов, имеющих положи­тельные времена ожидания, тогда определяется согласно уравнению (3.11):

или, если мы обозначаем вероятность положительного времени ожидания {1 — IV (0)} буквой D (вероятность задержки), то:

Z) • {1 - W+ (t)} = 1 - W_s(t). (3.18)

Тогда для функции плотности мы имеем согласно (3.11):

D ' w+ (0 = w_s(t). (3.19)

Средняя величина распределения получается:

D-w= W, (3.20)

где средняя величина для всех клиентов обозначена W, и средняя величи­на для задержанных клиентов обозначена w. Формула действительна для любой системы с бесконечной очередью.

2. Нагрузка по времени пребывания в системе продолжительностью меньше, чем х

До сих пор мы не рассматривали важности времени «жизни» заявок от их продолжительности. Важность времени «жизни» часто пропор­циональна его продолжительности, например, когда мы рассматриваем нагрузку системы с организацией очереди, затраты времен центрального процессора, сеанс телефонной связи и т.д.

Если мы распределяем коэффициент веса времени «жизни» про­порционально его продолжительности, то средний вес всех временных интервалов становится равным средней величине

ос

«=JV(/)d/, (3.21)

о

^ГД^&f(t)dt — вероятность наблюдения в пределах интервала (t, t + dt)nt — вес этого наблюдения.

При обработке нагрузки нас интересует вычисление соотношения ^Всей нагрузки, которая возникает в системе, и времени пребывания в системе заявок продолжительностью меньше, чем х:

х

Р_х= (3.22)

Это то же самое, что и соотношение средней величины нагрузки, которая возникает в системе, и времени «жизни» меньше, чем х.

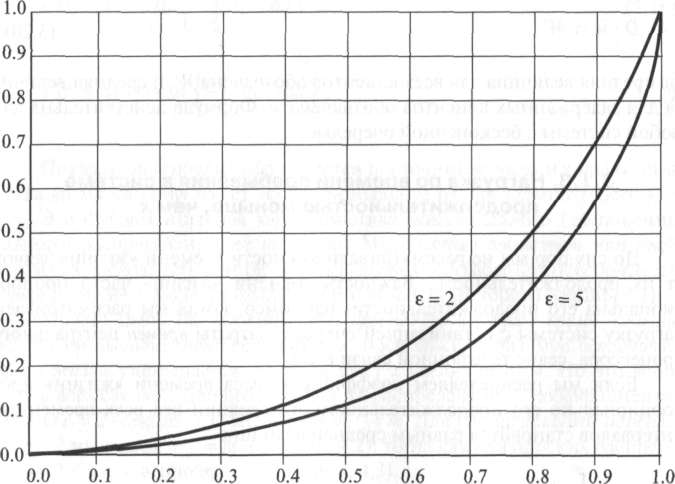
Часто относительно небольшое время обслуживания позволяет обслу­жить относительно большую долю полной нагрузки. Из рис. 3.2 мы видим, что если коэффициент формы е = 5, то 75% времен обслуживания вносят только 30%-ую долю полной нагрузки (правило Вильфредо Парето). Этот факт можно использовать и предоставлять приоритет коротким задачам без большой задержки более длинных задач (л екция 13).

Относительная нагрузка

Процент/100

Рисунок 3.2. Пример величины относительной нагрузки в зависи­мости от времени пребывания в системе, согласно уравнению (3.22). Здесь е = 2 соответствует показательному распределению, а е = 5 соответствует принципу Парето. Мы обращаем внимание, что 10% наибольших времен пребывания в системе вносят вклад от 33% до 47%, нагрузки (сравните математические ожидания времени обслу­живания клиента и среднее время ожидания в лекции 5)