Лекция 5. Процессы поступления заявок

Процессы поступления заявок, например, телефонных вызовов, при­бывающих на станцию, отображаются математически как стохастические точечные процессы. В случае точечного процесса нас интересуют лишь раз­ность между моментами поступления вызовов. Информация относительно одиночного поступления вызова (например, время обслуживания, число клиентов) игнорируется. Такая информация может использоваться только для того, чтобы определить, принадлежит ли поступивший вызов данному процессу или нет.

Математическая теория точечного процесса была разработана Пальмом в 1940 году. Эта теория нашла широкое применение во многих областях. Она была математически усовершенствована Хинчиным ([63], 1968) и стала широко применяться во многих учебных программах и учебниках.

1. Описание точечных процессов

Далее мы рассматриваем только простые точечные процессы, то есть, исключаем множественное прибытие, например, одновременное поступления двух вызовов. Для телефонных звонков это обеспечивается выбором достаточно малого интервала времени. Рассмотрим времена поступления вызова, где i-тый вызов поступает в момент времени Т.:

(5.1)

Первое наблюдение происходит в момент времени Т₀ = 0.

Число вызовов в полуоткрытом интервале [0, /]обозначим как N_t. Здесь - случайная переменная с непрерывными параметрами времени и дискретным пространством. С увеличением t N_tникогда не уменьшаются.

Интервалы времени между двумя последовательными поступления­ми заявок:

(5.2)

Это называется временем интервала, а распределение этого процесса называется распределением времени интервала.

Интервалы времени могут быть отображены двумя типами случай­ных переменных N_t и X., а два процесса могу быть охарактеризованы двумя способами.

1. Числовое представление N_t: при этом способе временной интервал t сохраняется постоянным, и мы наблюдаем случайную переменную N_t для числа вызовов в интервале t.

Накопленное число вызовов

Время (с)

Рисунок 5.1. Процесс поступления вызовов на входящих линиях транзитной станции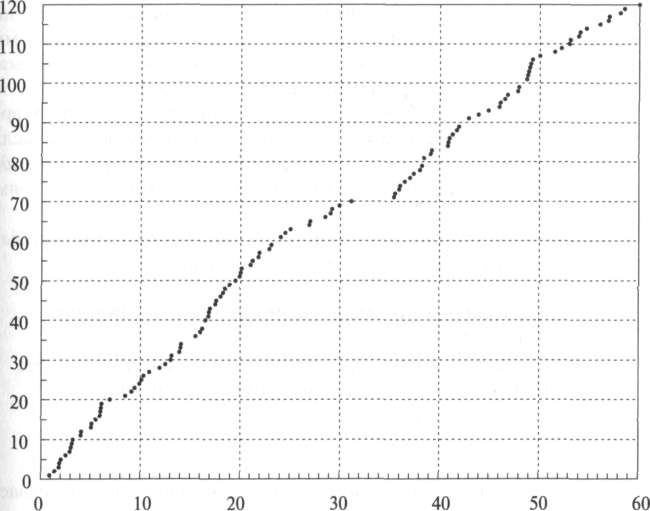

2. Представление с помощью интервала Т.: при этом способе число поступлений вызова сохраняется постоянным, а мы наблюдаем слу­чайную переменную Т. для временного интервала до тех пор, пока не поступят п заявок. Фундаментальные отношения между этими двумя представлениями отображаются следующим простым отношением:

Анализ точечного процесса может быть основан на обоих этих пред­ставлениях. В принципе, они эквивалентны. Представление с помощью интервала соответствует обычному анализу временных рядов. Если мы, например, рассмотрим /= 1, то получим математическое ожидание вызо­ва, иначе говоря, статистику, основанную на поступлении вызова.

Числовое представление не имеет никакой аналогии с анализом вре­менных рядов. Статистические данные, которые мы получаем, вычисля­ются в единицу времени, в результате получается математическое ожида­ние по времени (сравните разницу между потерями по вызовам и потерями по времени).

Статистика интересов при изучении точечных процессов может быть классифицирована согласно этим двум представлениям.