Используя диаграммы состояния, просто показать, что любой экспо­ненциальный временной интервал (А) может быть разложен на распреде­ления фазового типа (А), где Х.>Х. Что касается рис. 4.11, мы заметим, что интенсивность макросостояния (обведенный штриховой линией блок) X независима от микросостояния.

Рисунок 4.10. Гиперэкспоненциальное распределение с двумя фаза­ми (А, > Х₂, р₂ = 1-Pj) может быть преобразовано в распределение Кокса 2 (сравните с рис. 4.4)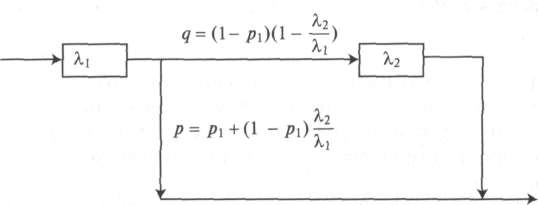

Когда число фаз к конечно и нет обратной связи, конечная фаза должна иметь интенсивность X.

Рисунок 4.11. Это распределение фазового типа эквивалентно един­ственному экспоненциальному распределению. Когда р. • Я,. = X. Соответственно А. > X и 0 < р. < 1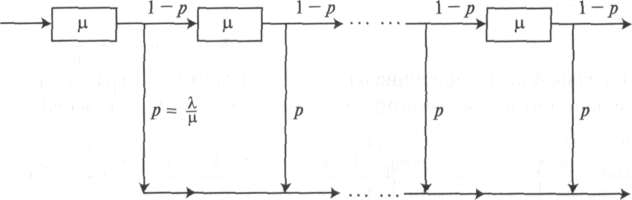

1. Важность Распределения Кокса

В последние годы распределения Кокса привлекли к себе большое внимание, поскольку они обладают следующими свойствами:

а. распределение Кокса может быть проанализировано с использова­нием метода фаз;

б. для произвольного распределения можно найти хорошее прибли­жение к распределению Кокса. Свойство, справедливое для распре-

деления Кокса, справедливо для любого распределения, имеющего

практический интерес.

Используя распределения Кокса, мы можем элементарными мето­дами получать результаты, которые раньше требовали очень сложной математики.

В практических приложениях теории мы использовали распреде­ления Кокса для получения методов оценки параметров. При решении статистической проблемы есть 2к параметра. Обычно мы можем выбрать специальное распределение Кокса (например, к-распределение Эрланга или гиперэкспоненциальное распределение) и приблизительный первый момент.

Применяя метод рулетки, мы с помощью числового моделирования на компьютерах автоматически получаем результаты наблюдений времен­ных интервалов в виде распределения Кокса с одной и той же интенсив­ностью для всех фаз.

4. Другие распределения времени

В принципе, каждое распределение, которое не имеет отрицательных значений, может использоваться как распределение времени и описывать временные интервалы. Но, практически, прежде всего востребованы вышеупомянутые распределения.

Мы предполагаем, что параметр ^-распределении Эрланга (4.8) принимает неотрицательные реальные значения, и получаем гамма- рас­пределение:

/(0 = -=тг;(^)*~¹-е~"-Х, X > 0, t> 0.

IW (4.39)

Средняя величина и дисперсия даются в (4.11) и (4.12).

Это распределение также известно в теории телетрафика как распре­деление Вейбулла.

Оно дает зависимость интенсивности времени отказа (3.14):

dF(t) _ taT<^w)* -k(\t)^k~^ldt

1. - F(t) ~ ^Ц(0 " e-<«>*

= Xk (4.41)

Распределение применяется в теории надежности. Для k = 1 мы Имеем экспоненциальное распределение.

Распределение Парето получается:

(4.42)

F(t) = 1 - (1 + ПоО ⁽¹⁺^ •

Средняя величина и коэффициент формы следующие:

1

*1- у,

А-Ло

(4.43)

Надо обратить внимание, что для Я < г|₀ дисперсия не существует. Если iy₍.—>0 (4.42), распределение становится экспоненциальным. Если интенсивность Пуассоновского процесса — гамма-распределеление, то времена между прибытиями распределены, согласно Парето.

Далее мы будем иметь дело с набором дискретных распределений, которые также описывают время жизни — такие, как геометрическое распределение, распределение Паскаля, биноминальное распределение, распределение Вестенберга и т.д. На практике параметры распределений не всегда постоянны.

Время обслуживание (удержания) может быть физически корре­лированным с состоянием системы. В системах человек/машина время обслуживания изменяется из-за занятости (уменьшается) или усталости (увеличивается). Электромеханические системы работают более медленно в течение периодов высокой нагрузки, потому что в это время наблюдает­ся уменьшение напряжения электрической сети.

Для некоторых распределений, которые широко применяются в тео­рии организации очереди, мы используем следующую систему сокращен­ных обозначений (сравните с секцией 13.1):

М - экспоненциальное (марковское) распределение,

Е_к — к-распределение Эрланга,

Н_п — гиперэкспоненциальное распределение порядка п,

D - (детерминированная) константа,

Сох — распределение Кокса,

G - общий - произвольное распределение.