1. Прерывистый Пуассоновский процесс

В секции 6.4 мы рассматривали прерывистый Пуассоновский процесс Качуры (IPP) (Kuczura, 1977 [71]), который характеризуется тремя пара­метрами и широко используется для моделирования нагрузки перегрузки. Возьмем полнодоступную группу с п обслуживающими приборами, на которые поступают вызовы, прибывающие согласно IPP (см. рис. 6.7) с экспоненциально распределенными временами обслуживания.

Тогда мы можем создать диаграмму переходов состояний, как пока­зано на рис. 9.6. Диаграмма двухмерная. Состояние (i, j) обозначает, что есть i обслуживаемых вызовов (/' = 0,1,..., п), а процесс поступления вызо­вов находится в фазе /'(/' = а, если идет процесс поступления вызовов, и j = b, если процесс возвращает вызов). Используя уравнения равновесия узлов, находим вероятности состояния равновесия p(i,j).

Потери по времени Е равны:

Потери по вызовам В равны:

(9.21)

Потери по нагрузке С определяются как соотношение предложенной нагрузки и потерянной нагрузки.

Предложенная нагрузка равна:

р(оп) X со Л,

p(on) + p(off) ц со+у ц'

Обслуженная нагрузка:

(9.22)

У = £ i' {Pi.ia) + РФ)) •

Из этого уравнения мы получаем С = (A - Y)/A. Фактически, потери по нагрузке будут равны потерям по вызовам, так как процесс поступле­ния вызовов является процессом рождения. Но это трудно вывести из полученных выше результатов. Как показано в секции 6.4.1, интервалы поступления распределены по гиперэкспоненте Н2.

Рисунок 9.6. Диаграмма переходов состояний для полнодоступ­ной системы с потерями с п обслуживающими приборами, IPP- процессом поступления вызовов (см. рис. 6.7) и экспоненциально распределенным временем обслуживания (|д)

2. Процесс поступления вызовов Кокс-2

В секции 6.4 мы отмечали, что процесс поступления вызовов Кокс-2 дает более общее представление процесса, чем IPP (Kuczura, 1977 [71]). Если мы рассматриваем процесс поступления вызовов Кокс-2, как пока­зано на рис. 4.10, то получаем диаграмму переходов состояний на рис. 9.7. Из неё мы находим, согласно предположению о статистическом равнове­сии вероятности состояния, следующие критерии качества работы: Потери по времени Е:

Е = р(па) + p(nb). (9.23)

Потери по вызовам В:

_{в =} Ph ‘р(па)+ Х₂ •р{пЪ) ^ ₂₄^

Ph ' Y^Piia) + Я.2 • ^РФ)

i=0 1=0

Потери по нагрузке С. Предложенная нагрузка - это среднее число среднего времени обслуживания, деленная на число попыток вызова. Средний интервал поступления:

0. , „ ,1 X₂ + (l -p)h т_а= т-+0 ~ Р)'т~ = •

Aj Л*2 А-2

Предложенная нагрузка тогда равна А = (т_а • ц)^-1. Обслуженная нагрузка определяется по (9.22) с помощью рис. 9.7, и таким образом мы находим потери по нагрузке С.

Если мы обобщим процесс поступления вызовов на процесс посту­пления вызовов Кокс-k, то диаграмма перехода состояний будет все еще двухмерной. При использовании распределения Кокса мы можем в прин­ципе рассматривать любое число параметров.

Если мы обобщаем время обслуживания с использованием распреде­ления Кокса- к, то диаграмма переходов состояний для п > 1 становится намного более сложной, потому что существует процесс обслуживания для каждого обслуживающего прибора, но только один процесс поступле­ния вызовов. Поэтому мы всегда обобщаем процесс поступления вызовов и принимаем экспоненциально распределенные времена обслуживания.

Л. А, К А.

Рисунок 9.7. Диаграмма переходов состояний для полнодоступной системы с потерями с п обслуживающими приборами, процесс поступления вызовов — Кокс-2 (см. рис. 4.10), и экспоненциально распределенным временем обслуживания (ц)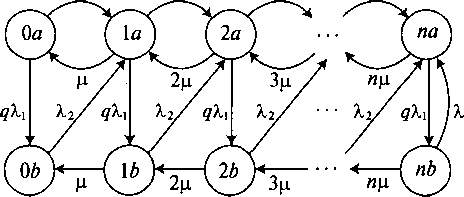

Краткие итоги

• В этой лекции рассматривались системы с ограниченной доступно­стью (неполнодоступные), то есть системы, где абонент или поток нагрузки имеют доступ только к к заданным каналам из общего количества п(к < п).

• В неполнодоступной системе, если все к каналы заняты, попытка вызова блокируется, даже если среди оставшихся (п—к) каналов есть свободные каналы.

• В сетях связи с альтернативной маршрутизацией нагрузка, которая потеряна первичной группой, предлагается группе перегрузки, и она имеет свойства, отличающие её от РСГ-нагрузки.

• В системе Костена группа разбита на ограниченную первичную группу с я каналами и группой перегрузки с бесконечной емкостью, предлагаемая нагрузка — РСТ 1.

• Объединенный процесс перегрузки g потоков нагрузки называют эквивалентной нагрузкой перегрузки от единственной полнодоступ­ной группы с тем же самым математическим ожиданием и дисперси­ей нагрузки перегрузки.

• При применении метода ERTмы должны вычислить (т, v) для дан­ных значений (А, п) и наоборот. Это требует применение итерацион­ной процедуры.

• Мы можем разбить полную потерянную нагрузку на отдельные пакеты потерянной нагрузки, принимая во внимание, что нагрузка, потерянная для потока /, пропорциональна т. — средней величине и пиковости потока Z. = v/m. (Нагрузка) вероятность блокировки для нагрузки потока / называется вероятностью блокировки пакета.

• Фредерикс (1980 [29]) предложил метод эквивалентности. Для пико­вости Z* 1 метод Фредерикса и Хэйварда предполагает, что система имеет такую же вероятность блокировки, как система из n/Zканалов с предложенной нагрузкой А/Z, и таким образом пиковость Z= 1. Для последней системы мы можем применить В-формулу Эрланга, при этом следует учитывать, что В-формула Эрланга работает для непре­рывного числа каналов.

• Башарин и Куренков расширили метод, включив мультислотовую (мультискоростную) нагрузку, где вызов требует d каналов от своего начала и до завершения. Если вызов использует d каналов вместо одного (изменение масштаба), то средняя величина времени стано­вится в d раз больше и дисперсия времени - больше в d² раз.

• Если нам необходима большая пропускная способность сети, чем предоставляет одиночный канал, то можно параллельно комбини­ровать больше каналов. В первоначальном источнике мы можем распределить нагрузку (пакеты или ячейки в ATM) циклическим способом по отдельным каналам и в пункте назначения - восстано­вить первоначальную информацию.

• ВРР-модели нагрузки описывают нагрузку двумя параметрами: сред­ней величиной и пиковостью.

• Метод Сандера преобразовывает не-Пуассоновскую нагрузку (сред­нее значение, дисперсия = т; v) в нагрузку потока с пиковостью Z, прибавляя постоянный поток (нулевая дисперсия) нагрузки со средним значением v-m так, чтобы полная нагрузка имела среднее значение, равное дисперсии v.

• Если мы рассматриваем полнодоступную группу с п обслуживающи­ми приборами, на которые поступают вызовы, прибывающие соглас­но IPP с экспоненциально распределенными временами обслужива­ния, то можем создать диаграмму переходов состояний. Состояние (/, j) обозначает, что есть i обслуживаемых вызовов (/' = 0,1,..., и), а процесс поступления вызовов находится в фазе j (J = а, если идет процесс поступления вызовов, и j = Ь, если процесс возвращает вызов). Используя уравнения равновесия узлов, мы находим вероят­ности состояния равновесия р (i,j).

Лекция 10. Многомерные системы с потерями

В этой лекции мы обобщаем классическую теорию телетрафика на решение задач в мультисервисных системах (например, цифровые сети инте­грального обслуживания ISDN а В ISDN). Каждый класс услуг соответствует потоку нагрузки. Несколько потоков нагрузки предлагаются одной и той же группе пучков каналов.

В секции 10.1 мы рассматриваем классическую многомерную В-формулу потерь Эрланга. Это пример обратимого марковского процесса, который мы рассмотрим более детально в секции 10.2. В секции 10.3 мы проанализи­руем большее количество общих систем с потерями и стратегий, включая сервисную защипу (максимальное распределение каналов между сервисами) и мультислотовую нагрузку (ВРР). Все модели имеют так называемую муль­типликативную форму (форму произведения - product form), и их числовая оценка очень упрощается при использовании алгоритма свертки для систем с потерями, реализованных специальной программой (секция 10.4). В сек­ции 10.5 будут приведены другие алгоритмы для решения этой проблемы.

Все модели, которые мы рассматриваем, основаны на гибком распре­делении каналов/слотов. Они могут быть обобщены на произвольные сети коммутации каналов с прямой маршрутизацией, где мы вычисляем вероят­ности блокировки из конца в конец (лекция 11). Все модели нечувствительны к распределению времени обслуживания, и таким образом они устойчивы для приложений. В конце лекции поговорим о других алгоритмах.

10.1 Многомерная В-формула Эрланга

Мы рассматриваем группу п пучков каналов (каналы, слоты), кото­рым предлагают два независимых PCT-I потока нагрузки: (Х_г )i₍) и (К₂, щ). Предлагаемая нагрузка А_] - А., соответственно А₇ = \ /ц .

Обозначим состояние системы(/,у), где i - число вызовов от потока 1, a у — число вызовов от потока 2. Выполняются следующие ограничения:

О < г < п,

О < j < п, (10.1)

0 < / + у < п.

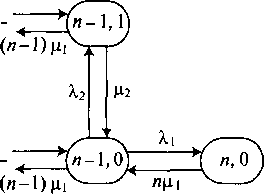
Диаграмма переходов состояний показана на рис. 10.1. Согласно предположению о статистическом равновесии, вероятности состояний могут быть получены решением глобальных уравнений равновесия для каждого узла (уравнения узла), всего (« + !)(« + 2)/2 уравнения.

Рисунок 10.1. Двухмерная диаграмма переходов состояний для систе­мы с потерями с п каналами, которым предлагают два РСТ- / потока нагрузки. Это эквивалентно диаграмме переходов состояний для системы с потерями М/Н₂/п, где гиперэкспоненциальное распреде­ление Н₁ дается в (10.7)

Как мы увидим в следующей секции, эта диаграмма соответствует обратимому марковскому процессу, который имеет локальное равновесие и, кроме того, решение имеет форму произведения (product form). Мы можем легко показать, что глобальные уравнения равновесия удовлетво­ряют следующим вероятностям состояния, которые могут быть записаны в форме произведения: