Пример 6.2.2: Спутниковая система синхронного (сегментированная) алоха

ALOHA — метод случайного доступа, принцип которого состоит в том, что все станции работают в одном канале связи, контролируя его работу, а передача осуществляется в случайные моменты времени. Когда две или более станций передают пакет в один и тот же момент времени (или перекрывавшиеся интервалы), приемник оказывается не способен правильно его принять. Поэтому при возникновении подобных ситуаций осуществляется повторная передача пакетов через случайный интервал времени. Различают два метода доступа: «чистая» (несегментированная) АЛОХА и сегментированная синхронная АЛОХА. В первом случае повто­

рение передачи осуществляется в случайное время, во втором - в син­хронные промежутки времени.

Рассмотрим цифровую спутниковую систему связи с постоянной длиной пакета И.

Спутник находится на геостационарной позиции приблизительно в 36.000 км выше уровня экватора, так что задержка распространения туда и обратно - приблизительно 280 мсек., а ось времени разделена на слоты фиксированной продолжительности, соответствующей длине пакета И.

(6.19)

150

Это соответствует соотношению осей времени, которое используется эффективно. Эта функция, как показывает рис. 6.4, имеет оптимум для Xh = 1, так как производная по А.И равна нулю.

-				©	©	©	900 наблюдений X = 6.39 © Теоретически
о							©
-
		©
									-	©
■сг	“Г-1		г		1		1		1		ТГ © н-—f 91 и чв ■

100

75

50

25

Число наблюдений

125

10

12 14 16 18 Число вызвов в сек

Рисунок 6.3. Число вызовов в секунду для автоматического соеди­нения с набором номера. Теоретические значения получены при условии Пуассоновского распределения. При статистических испы­таниях принята гипотеза Пуассоновского распределения

Для этих условий:

p'_xh(l)= -(I-Xh), (6.21)

Мах{/>(1)} = е'¹ = 0.3679. (6.22)

Таким образом, имеем максимальное использование канала, рав­ное 0.3679, когда в среднем мы передаем один временной слот на пакет. Подобный результат сохраняется, когда число терминалов ограничено, и число временных слотов на пакет распределено биноминально.

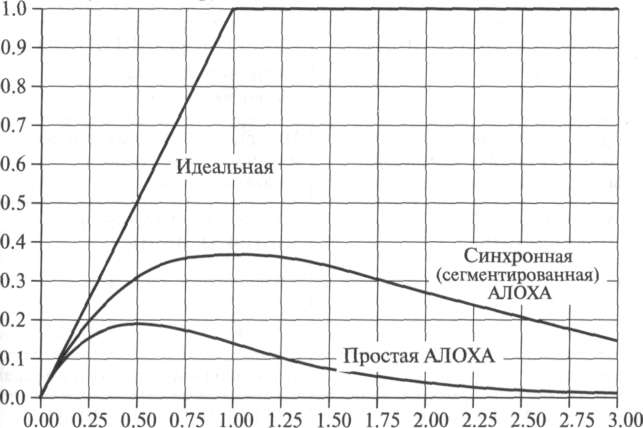
Обслуженная нагрузка

Предложенная нагрузка

Рисунок 6.4. Обслуженная нагрузка в системе синхронной (сегмен­тированной) AJIOXA имеет максимум (пример 6.2.2). С простым протоколом АЛОХА мы будем иметь дело в примере 7.2.1.