ОСНОВИ ТЕХНІЧНОЇ МЕХАНІКИ

Практичні роботи

Спеціальність 5.05070103 “Електропостачання”

ПРАКТИЧНА РОБОТА№__

Тема: Плоска система збіжних сил.

Мета: навчитися складати рівняння рівноваги для плоскої системи збіжних сил, знаходити зусилля в стержнях.

Теоретичне обґрунтування

Системою збіжних сил називають таку систему сил, лінії дії яких перетинаються в одній точці. Якщо лінії дії збіжних сил розташовані в одній площині, то маємо плоску систему збіжних сил. Якщо лінії дії цих сил розташовані у різних, непаралельних площинах, то маємо просторову систему збіжних сил. Точку прикладання сили, згідно з першим наслідком аксіом статики, можна перенести у будь-яку іншу точку вздовж лінії дії цієї сили. Це дає змогу систему збіжних сил замінити еквівалентною системою сил, які прикладені в одній точці. Для рівноваги плоскої системи збіжних сил необхідно і достатньо, щоб силовий многокутник, побудований на цих силах, був замкнутим (тоді рівнодіюча системи сил буде дорівнювати нулю). Це геометрична умова рівноваги плоскої системи збіжних сил.

Аналітична умова рівноваги плоскої системи збіжних сил: для рівноваги плоскої системи збіжних сил необхідно і достатньо, щоб алгебраїчна сума проекцій усіх сил системи на кожну з двох осей координат дорівнювала нулю.

Рівняння рівноваги у цьому випадку мають такий вигляд :

Проекція вектора сили на будь-яку вісь дорівнює добутку модуля цієї сили на косинус кута між напрямом сили і додатним напрямом осі.

Якщо кут гострий (˂ 90°) то проекція додатна; для тупого кута - проекція від’ємна.

Якщо сила F перпендикулярна до осі (= 90°), її проекція на вісь дорівнює нулю.

Якщо сила F паралельна осі (= 0° або = 180°), то вона проецирується на цю вісь у натуральну величину.

Послідовність рішення задач

• Виділити точку або тіло, рівновагу яких треба розглянути для розв’язання даної задачі.

• Зобразити активні сили.

• Звільнити цю точку або тіло від в’язей і замінити їх дію силами реакцій в’язей.

• Вибрати систему координат і скласти силову схему.

• Скласти необхідні й достатні рівняння рівноваги відповідно до розташування сил, що прикладені до точки або тіла.

• Розв’язати рівняння рівноваги та визначити невідомі величини.

• Зробити перевірку правильності знайдених величин.

Питання для самоконтролю

10. Яка система сил називається збіжною?

11. Які є системи збіжних сил ? Наведіть приклади найпростіших систем збіжних сил (плоскої і просторової).

12. Сформулюйте правила побудови силового трикутника, паралелограма, паралелепіпеда і многокутника.

13. Графічна і аналітична умови рівноваги плоскої системи збіжних сил.

14. Чи може вільне тверде тіло знаходитися в рівновазі під дією :

А) однієї сили; б) двох сил; в) трьох сил ?

10. Що називається проекцією сили на вісь?

11. Як напрямлена сила F, якщо відомі її проекції на осі координат: А)F_х=0, F_У=F; б)F_х=-F, F_у= 0; в)F_х=F_у; г)F_х = -F_у.

8. Скільки і які можна скласти рівняння рівноваги для плоскої системи

збіжних сил ?

10. Що являється геометричною умовою рівноваги для плоскої системи збіжних сил ?

11. Яка сила називається рівнодіючою ?

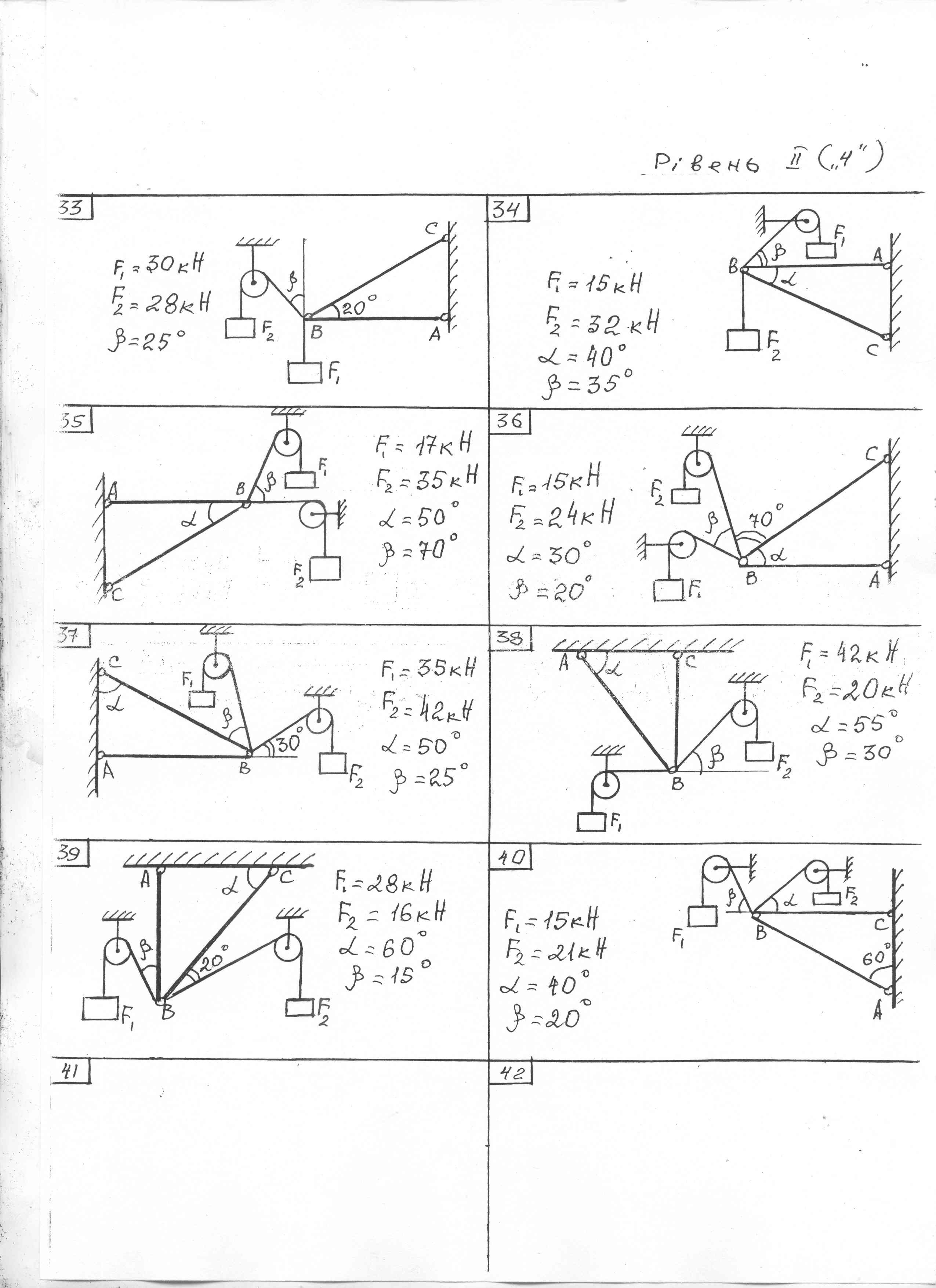
Завдання для самостійної практичної роботи №1:

Стержні АВ і ВС з’єднані шарніром В, на вісь якого діють навантаження. Кріплення стержнів у точках А і С шарнірні. Визначити зусилля в стержнях. Дані для свого варіанту взяти із малюнку №1.

Задача 1.

Стержні АВ і ВС з'єднанні шарніром В і підтримують навантаження F₁ і F₂. Визначити реакції в стержнях, якщо F₁ = 10 кН; F₂ = 7 кН.

Рішення.

Рішення :

1. Розглядаємо рівновагу шарніра В.

2. Звільняємо шарнір В від в'язей, зображаємо діючи на нього активні сили F₁, F₂ і реакції в'язів R_AB, R_BC.

3. Вибираємо систему координат і складаємо рівняння рівноваги для системних сил, які діють на шарнір В.

1. ƩX_і = 0; F₂ x соs 60° — R_AB — R_BC x cos 40° = 0;

2. ƩУ_і = 0; F₂ х соs 30° — F₁ — R_BC x соs 50° = 0;

Із рівняння (2) маємо:

Отримане рішення підставляємо в рівняння (1) і визначаємо реакцію R_АВ.

Перевірка: вибравши нове роз^положення осей координат х,у, складаємо рівняння:

Значить, реакції стержнів визначені вірно, знак - вказує, що реакція R_вс має протилежний напрям.

Практична робота №___

Тема: Визначення опорних реакцій двохопорних балок.

Мета: засвоєння методики розвя’зання задачі, формування практичних навичок по складанню рівнянь рівноваги і рішення цих рівнянь.