2. Порядок виконання роботи

1.Запустіть Deductor Studio.

2.Імпортуєте файл «bicycle_sales.txt:» (а потім свій варіант).

3.Застосуйте до імпортованої гілки обробник «Ассоциативные правила».

4. Створіть дерево асоціативних правил.

5. Створіть візуалізатор «Что-если».

6. Застосуйте обробники: «Группировка», «Калькулятор», «Слияние с узлом», «Сортировка», «Скрипт».

7. Обчисліть ліфт асоціативних правил.

8. Побудуйте OLAP – куб для асоціативних правил.

9.Проведіть інтерпретацію правил.

2. Звіт про лабораторну роботу

Звіт містить наступні результати:

1.Титульний лист.

2.Мета роботи.

3.Варіант студента.

4.Опис кожного зробленого завдання згідно свого варіанту;

5.Скриншоти кожного зробленого завдання згідно свого варіанту;

6.Висновки.

2. Контрольні запитання

1. Якими показниками характеризується асоціативні правила?

2. Що таке асоціативні правила?

3. Що таке дискретні дані?

4. Що таке артефакт?

Лабораторна робота №7.

Нейронні мережі в аналітичній платформі Deductor.

Мета роботи: навчитися будувати нейронні мережі в аналітичній платформі Deductor.

1. Загальні методичні рекомендації

Побудова нейронної мережі в платформі Deductor включає в себе декілька кроків.

Перший крок - імпорт даних в Deductor. Пригадаймо, що у поставці Deductor Асаdemic 5.1 імпортувати можна як з текстового файлу, так із сховища даних. Імпорт виконується кнопкою . При потребі над даними можна виконати певні операції: очистку та трансформацію даних. Робиться це кнопкою «Мастер обработки» .

Другий крок. Для побудови власне нейромережі слід кнопкою «Мастер обработки» запустити відповідний обробник (рис. 7.1).

Рис. 7.1. Запуск обробника «Нейросеть».

В подальшому потрібно задати налаштування нейромережі, що здійснюється в декілька кроків:

• Вказати, які поля є вхідними, вихідними, інформаційними та які взагалі не використовувати при побудові моделі. Для даних, що використовувалися в лабораторній роботі 5 (дані про абонентів компанії мобільного зв'язку) це матиме наступний вигляд - рис. 7.2. Всі суттєві поля є вхідними (крім «Код»), а те, яке потрібно спрогнозувати - вихідним (в даному випадку це «Середньомісячні витрати»).

• На слідуючому кроці здійснюється розподіл всієї множини на навчальну та тестову. Значення, вказані по замовчуванню, можна залишити без змін.

• На наступному (рис. 7.3) кроці задаються параметри, що визначають структуру нейронної мережі, - кількість прихованих слоїв і нейронів в них, а також активаційна функція нейронів. В секції «Нейроны в слоях» необхідно вказати кількість прихованих слоїв, тобто слоїв нейронної мережі, розташованих між вхідним і вихідним слоями. Для цього в полі «скрытых слоев» вказати відповідне значення. Число нейронів у вхідному і вихідному слоях автоматично встановлюється відповідно до числа вхідних і вихідних полів навчальної вибірки і тут змінити його не можна.

Важливе зауваження: до вибору кількості прихованих слоїв і кількості нейронів для кожного прихованого слою потрібно підходити обережно. Хоча і не вироблені чіткі критерії вибору, дати декілька загальних порад все ж можна. Вважається, що задачу будь-якої складності можна вирішити за допомогою двослойної нейромережі, тому конфігурація з кількістю прихованих слоїв, що перевищують 2, навряд чи виправдана. Для вирішення багатьох завдань цілком підійде й однослойна нейронна мережа. При виборі кількості нейронів слід керуватися наступним правилом: «кількість зв'язків між нейронами повинна бути приблизно на порядок менше кількості прикладів в навчальній множині». Кількість зв'язків розраховується як сума зв'язків кожного нейрона зі всіма нейронами сусідніх слоїв, включаючи зв'язки на вхідному і вихідному шарах. Дуже велика кількість нейронів може призвести до так званого «перенавчання» мережі, коли вона видає добрі результати на прикладах, що входять в навчальну вибірку, але практично не працює на інших прикладах.

В розташованій нижче таблиці (рис. 7.3), для кожного прихованого слою необхідно вказати число нейронів, що входитимуть в нього. В секції «Активационная функция» необхідно визначити тип функції активації нейронів та її крутизну. В нижній частині вікна відображається графік вибраної функції відповідно до встановленої крутизни.

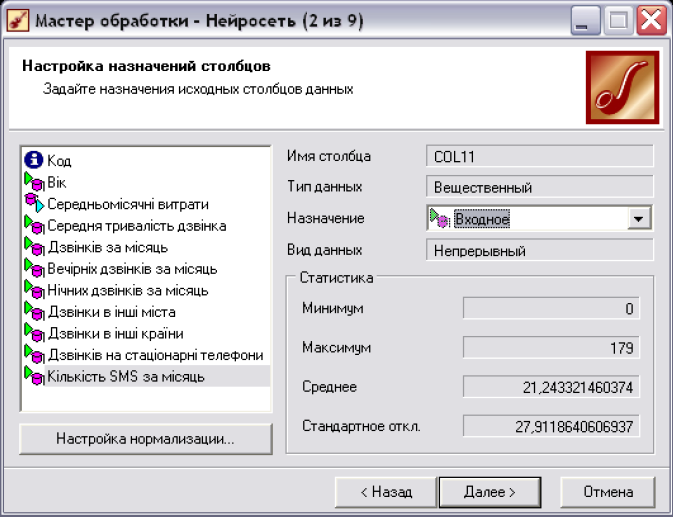
Рис. 7.2. Задання призначення полів в нейронній мережі.

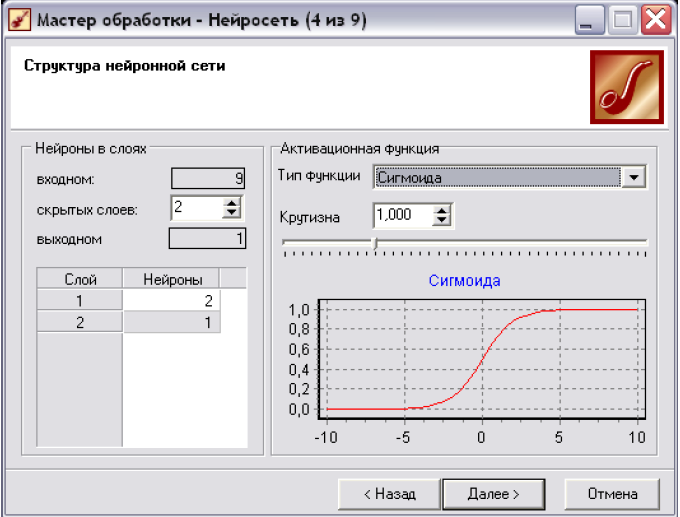
Рис. 7.3. Визначення слоїв нейронної мережі.

• Наступний крок (рис. 7.4) - налаштування процесу навчання нейронної мережі.

Можна вибрати два способи: Васk-Ргораgation (зворотнє розповсюдження помилки) та Resilient Ргораgation (еластичне розповсюдження помилки). Кожен метод має по два параметри. Васk-Ргораgation: 1)«Скорость обучения» -визначає величину кроку при ітераційній корекції вагів в нейронній мережі (рекомендується задавати в інтервалі (0,1) та 2) «Момент» - враховує величину останньої зміни ваги при корекції ваг (задається в інтервалі (0,1). Resilient Ргораgation: 1) «Шаг спуска» - коефіцієнт збільшення швидкості навчання, який визначає крок збільшення швидкості навчання при недосягненні алгоритмом оптимального результату та 2) «Шаг подьема» - коефіцієнт зменшення швидкості навчання, задається крок зменшення швидкості навчання в разі пропуску алгоритмом оптимального результату.

• На слідуючому - шостому - кроці побудови нейронної мережі вказується параметри, при виконанні яких навчання мережі буде зупиненою (рис. 7.5). Головні з них:

а. «Считать пример распознанньм, если ошибка меньше» - критерієм зупинки в даному випадку є умова, що різниця між еталонним і реальним виходом мережі стає менше заданого значення.

Ь. «По достижении эпохи» - встановлений прапорець дозволяє задати число епох (циклів навчання), після досягнення якого навчання зупиняється незалежно від величини помилки.

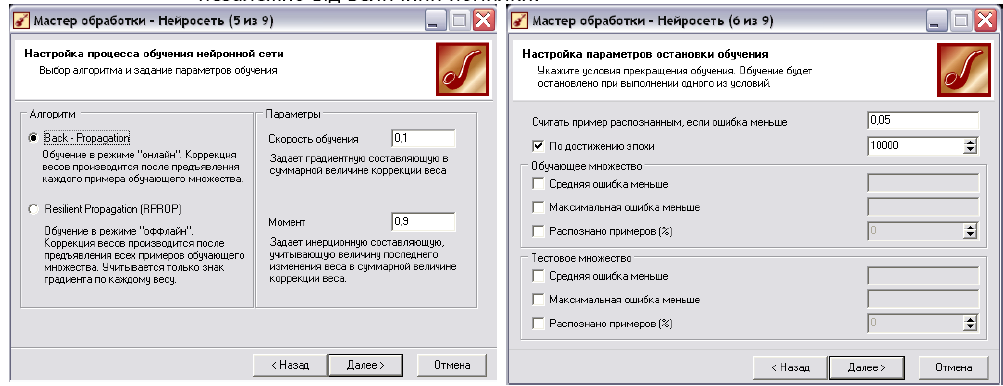
Рис. 7.4. Налаштування процесу навчання нейронної мережі.

Рис. 7.5. Задання параметрів зупинки навчання нейронної мережі

• Слідуючий крок - проводить навчання нейронної мережі. При цьому в режимі on-linе можна слідкувати за самим процесом та його ключовими показниками (рис. 7.6). Навчання вважатиметься успішним, якщо відсоток розпізнаних прикладів в навчальній та тестовій множинах достатньо великий (близький до 100%). В процесі навчання у вікні відображаються наступні графіки ходу навчання для навчальної (синя лінія) та тестової (червона лінія) множин: 1) максимальна квадратична помилка для навчальної та тестової множини (суцільна лінія); 2) середнє квадратичне відхилення для навчальної множини та тестової множини (пунктирна лінія).

• Передостанній крок задає, яким чином буде візуалізуватися нейронна мережа. Рекомендується вибрати так, як показано на рис. 7.7.

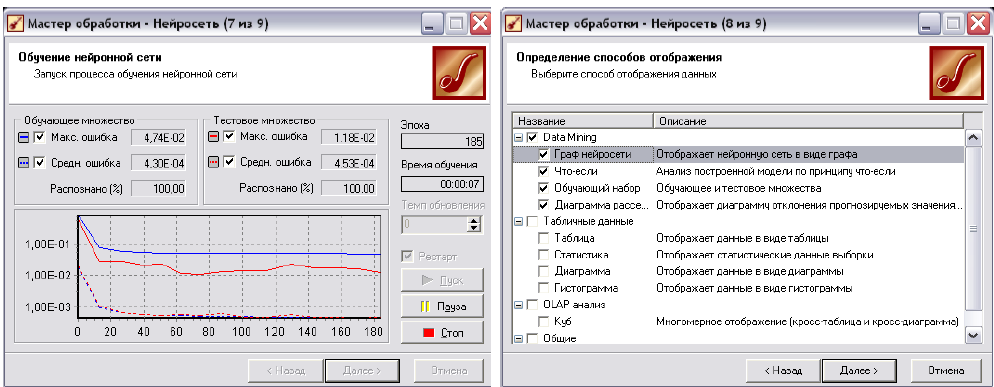
Рис. 7.6. Навчання нейронної мережі.Рис. 7.7. Візуалізація нейронної мережі

Нижче розглянемо призначення кожного з візуалізаторів:

■ «Граф нейросети» - дозволяє графічно представити нейронну мережу з усіма її нейронами і синапсичними зв'язками. При цьому можна побачити не тільки структуру нейронної мережі, але і значення вагів, які приймають ті або інші нейрони. Залежно від ваги нейрона він відображається певним кольором, а відповідне значення можна визначити за колірною шкалою, розташованою внизу вікна (рис. 7.8).

■ «Что-если» - аналіз по методу «Что-если» дозволяє визначити, як поводитиме себе побудована модель при подачі на її вхід нових даних. Простіше кажучи, проводиться експеримент, в якому, змінюючи значення вхідних полів нейронної мережі користувач спостерігає за зміною значень на виході (рис. 7.9).

■ «Обучающий набор» - являє собою таблицю даних, на основі яких будувалася нейронна мережа. Використовуючи кнопки на панелі інструментів можна проводити маніпуляцію над даними. Жовтим кольором в таблиці відображаються рядки, які попали в тестову множину. За допомогою кнопки «Исходный набор данных» , можна окремо відобразити навчальну та тестову множини.

■ «Диаграмма рассеяния» - діаграма розсіювання служить для наочної оцінки якості навчання моделі за допомогою результатів порівняння значень вихідного поля і значень того ж поля, але розрахованих моделлю. На діаграмі розсіювання відображаються вихідні значення для кожного з прикладів навчальної вибірки, координати яких по осі Х - це значення виходу в навчальній вибірці (еталон), а по осі У - значення виходу, розраховане навченою моделлю на тому ж прикладі. Пряма діагональна лінія є орієнтиром (лінію ідеальних значень). Чим ближче точка до цієї лінії, тим менше помилка моделі. Протягуванням лівою кнопкою миші вправо на потрібній частині діаграми можна збільшити її масштаб, а протягування вліво - зменшити його.

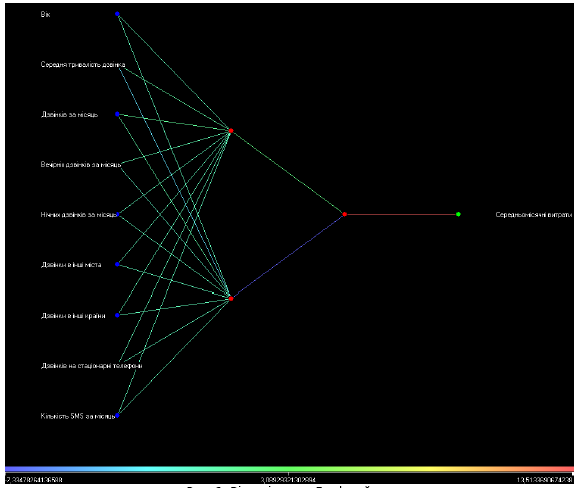
Рис. 7.8. Візуалізатор «Граф нейросети».

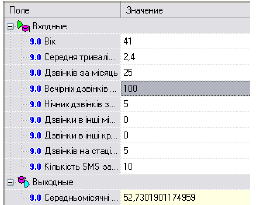
Рис. 7.9. Візуалізатор «Что-если».

Рис. 7.10. Візуалізатор «Диаграмма рассеяния».

Увага!!! Для одного і того ж набору даних варто будувати нейронні мережі з різними параметрами: кількістю прихованих слоїв та нейронів в них (рис. 7.3); різним алгоритмами навчання та їхніми параметрами (рис. 7.4).

Після побудови декількох нейронних мереж можна оцінити їхню якість. Яким чином? Для цього слід проаналізувати діаграму розсіювання.

Припустімо, що рівень помилки, який нас влаштовує становить 0,01. За допомогою кнопки вказуємо потрібне значення для діаграм розсіювання всіх побудованих нейромереж. Оптимальною вважається та нейромережа, на діаграмі розсіювання якої найменша кількість точок виходить за межі ліній помилки (червоні пунктирні лінії). З рис. 7.11а та 7.11б видно, що кращою є та нейромережа, для якої характерна діаграма розсіювання на рис. 7.11б.

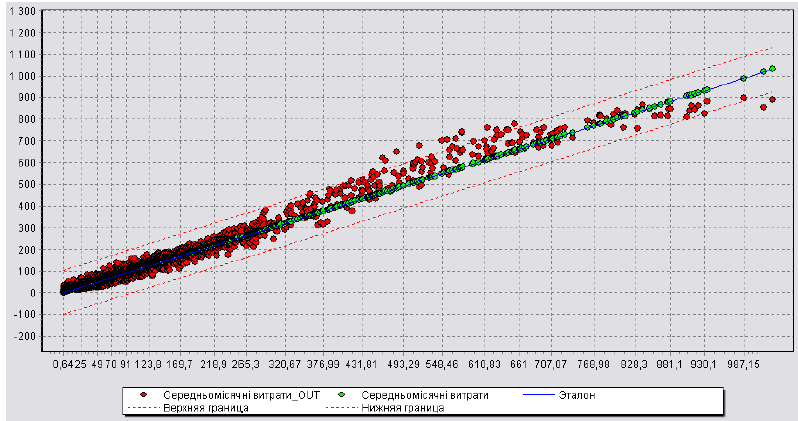
Рис.7.11а. Діаграма розсіювання для нейромережі архітектури (9x2x1x1), що прогнозує витрат абонентів компанії мобільного зв'язку.

Рис. 7.116. Діаграма розсіювання для нейромережі архітектури (9x2x1), що прогнозує витрат абонентів компанії мобільного зв'язку.

Подібний аналіз (тільки вже не візуальний, а чисельний) можна провести за допомогою вікна «Оценка качества модели» (рис. 7.12а), яке відкривається кнопкою на панелі інструментів діаграми розсіювання.

Суть діаграми, яка зображена в даному вікні наступна: по осі X - відкладається значення відхилень вихідних показників, що визначає модель до реальних вихідних показників з начальної вибірки (всі значення - в експоненціальній формі, наприклад, 2,ОЕ-О3=0,002); по осі Y вказується кількість записів, у яких помилка потрапляє у відповідний інтервал помилок на осі X. В дужках відображається відсоток, який складають ці записи у всьому наборі.

Червоним кольором показана гістограма щільності розподілу помилок, синім кольором - емпірична функція розподілу помилок.

Як же за допомогою даної діаграми оцінити якість побудованої моделі? Розглянемо рис 7.12а та 7.126, які відповідно побудовані для нейромережі архітектури 9x2x1x1 та нейромережі з архітектурою 9x2x1. Обидві мережі прогнозують середні витрати абонента компанії мобільного зв'язку.

Як видно з рис. 7.12а, для моделі на основі нейромережі 9x2x1x1: 97% всіх значень мають рівень помилки, який нижчий від 0.002; ще 2% значень мають показник помилки в інтервалі (0.002, 0.004] і ще приблизно для 2% значень цей показник перевищую 0.004.

В той же час для моделі, що побудована на основі архітектури 9x2x1 маємо: 99% - значень з рівнем помилки до 0.0027 та 1% - з рівнем, що перевищує 0.0027. Тому можна однозначно стверджувати, що більш оптимальною є модель побудована на основі нейромережі з архітектурою 9x2x1. Саме на основі цієї мережі (на закладці «Что-если») і слід прогнозувати вихідні значення.

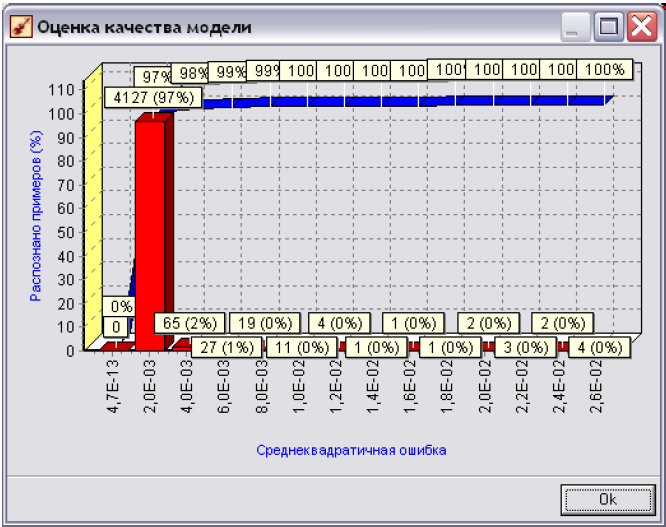
Рис. 7.12а. Діаграма оцінки якості моделі для нейромережі архітектури (9x2x1x1), що прогнозує витрат абонентів компанії мобільного зв'язку.

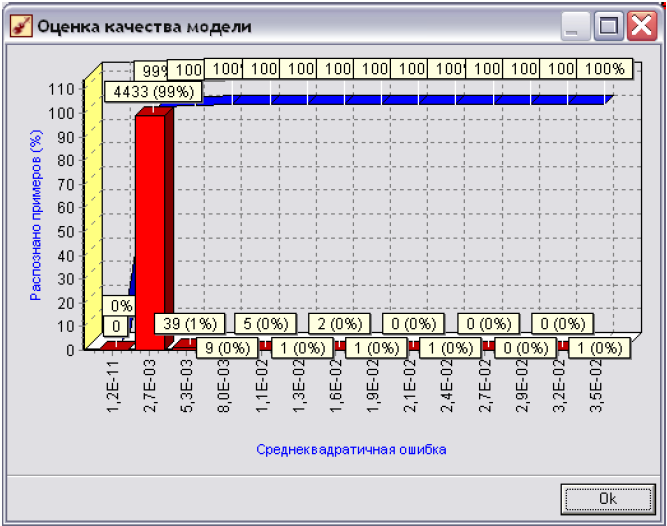
Рис. 7.12б. Діаграма оцінки якості моделі для нейромережі архітектури (9x2x1), що прогнозує витрат абонентів компанії мобільного зв'язку.