22. Винтовые поверхности

Винтовой поверхностью называется поверхность, которая описы­вается какой-либо линией (образующей) при ее винтовом движении.

Если образующей винтовой поверхности является прямая линия, то поверхность называется линейчатой винтовой поверхностью или ге­ликоидом Геликоид назы­вается прямым или наклонным в зависимости от того, перпендикулярна образующая оси геликоида или наклонна.

виды линейчатых винтовых поверхностей:

1) Прямой геликоид

2) Наклонный геликоид

3) Развертывающий геликоид

Если образующая l пересекается с осью поверхности, геликоид называется закрытым. Если образующая l не пересекается с осью поверхности, геликоид называется открытым.

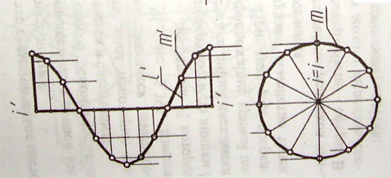
23. Линии пересечения, получаемые при пересечении прямого кругового конуса плоскостью

В зависимости от направления секущей плоскости в сечении ко­нуса вращения могут получиться различные линии. Они называются ли­ниями конических сечений.

Если секущая плоскость проходит через вершину конуса, в его се­чении получается две прямые — образующие (треугольник) В результате пересечения конуса плоскостью, перпендикулярной оси конуса, получается окружность. Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении конуса могут получиться эллипс, парабола или гипербола - в зависимости от величины угла наклона секущей плоскости.

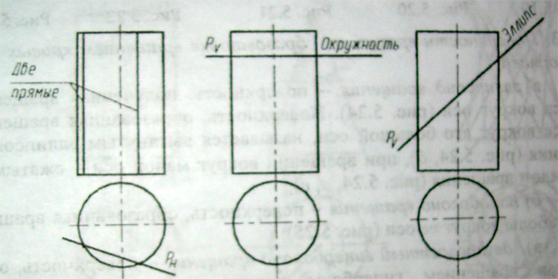
24. Линии пересечения, получаемые при пересечении прямою кругового цилиндра плоскостью.

При пересечении цилиндра вращения плоскостью, параллельной оси вращения, в сечении получаются две прямых – образующих. Если секущая плоскость перпендикулярна оси вращения, в результате сечения получится окружность. В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сече­нии получается эллипс.

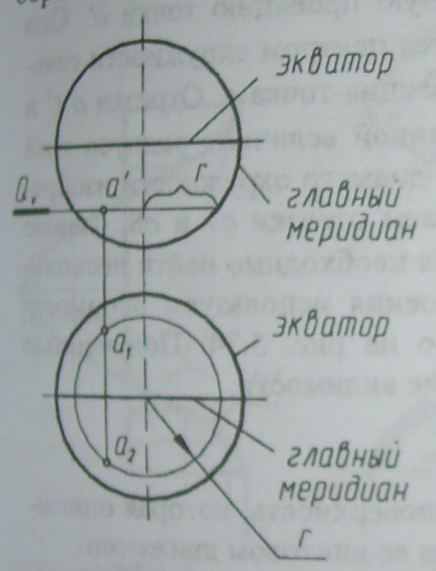
25. Линии пересечения, получаемые при пересечении сферы плоскостью.

Шаровой поверхностью (или сферой) называется поверхность, образованная при вращении окружности вокруг своего диаметра.

Если шаровая поверхность пересе­кается плоскостью, то в сечении всегда получается окружность. Эта окружность может спроецироваться:

- в прямую, если секущая плоскость перпендикулярна плоскости проекций;

- в окружность с радиусом, равным расстоянию от оси вращения шара до очерка.

- в эллипс, если секущая плоскость не параллельна плоскости проекций.

Чтобы построить проекции точки, лежащей на поверхности шара, необхо­димо через нее провести секущую плоскость, параллельную плоскости проекций, затем построить окружность, на второй находится эта точка.

26. Линии пересечения, получаемые при пересечении гранного тела плоскостью.

В пересечении гранных поверхностей плоскостями получаются многоугольники. Их вершины опреде­ляются как точки пересечения ребер гранных поверхностей с секущей плос­костью.

Многоугольник сечения может быть построен двумя способами:

1. Вершины многоугольника нахо­дятся как точки пересечения прямых (ре­бер) с секущей плоскостью;

2. Стороны многоугольника нахо­дятся как линии пересечения плоскостей (граней) многогранника с секущей плос­костью.