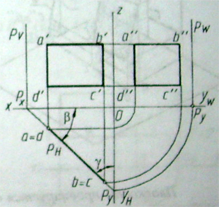
8. Теорема о проецировании прямого угла

Плоский угол в зависимости от положения по отношению к проекции может проецироваться от 0 до 180⁰

Плоский угол проецируется в натуральную величину, если его стороны параллельны плоскости проекции.

Если стороны плоского угла параллельны к плоскости проекции, то на эту плоскость проекции он проецируется в натуральную величину.

Проецирование прямого угла

Теорема. Прямой угол проецируется в виде прямого угла, если одна из его сторон параллельна плоскости проекций, а вторая ей не пер­пендикулярна.

Докажем это свойство проекций прямого, угла.

Доказательство. Пусть угол DEF=90° и расположен так, что обе его стороны параллельны плоскости Р. Тогда, как и всякая фигура, лежащая в плоскости, параллельной Р, данный угол спроецируется на Р без искажения, то есть его проекция угол def = 90°.

Через прямые EF и Ee проведем дополнительную плоскость Q. Плоскость Q перпендикулярна плоскости P.

Возьмем на перпендикуляре Ff какую - либо точку К и соединим ее с EЕ. Угол DEK тоже прямой, так как DEQ- Проекция угла DEK совпадает с проекцией угла DEF, так как точки F и K лежат на одном перпендикуляре к плоскости Р. Таким образом (угол) dek= def= 90°.

Но, как видно непосредственно из чертежа, только одна сторона DE угла DEK параллельна плоскости P.

Вторая сторона его EK наклонна к плоскости P.

Итак, для того чтобы прямой угол проецировался в натуральную величину, достаточно, чтобы одна его сторона была параллельна плос­кости проекций

9. Способы задания плоскости на чертеже .

На чертеже плоскость может быть задана несколькими способами:

а) проекциями трех точек, не лежащих на одной прямой;

б) проекциями прямой и точки, не лежащей на этой прямой;

в) проекциями двух пересекающихся прямых;

г) проекциями двух параллельных прямых;

д) проекциями любой плоской фигуры;

е) следами плоскости.

От одного задания плоскости можно пеейти к другому. В ряде случаев плоскость может быть изображена при помощи прямых, по которым она пересекает плоскости поекций.

Прямые, по которым плоскость пересекает плоскости проекций называют, следами плоскости.

Точки пересечения плоскости с осями проекци называются точками схода следов.

10. Частные случаи расположения плоскостей в пространстве и особенности их изображения на чертеже .

Виды плоскостей (по отношению к плоскостям проекции, плоскость может занимать сл. положения:

а) Плоскости уровня (плоскости || к плоскостям проекции)

б) Проецирующие (плоскости  к плоскостям проекции)

в) Наклонные (плоскости общего положения)

1) Горизонтально-проецирующая плоскость P(ABCD)H

2) Фронтально-проецирующая плоскость Q(ABCD)V

3) Профильно-проецируещая плоскость T(ABCD)W

1) Горизонтальная плоскость P(ABCD)||H

2) Фронтальная плоскость Q(ABCD)||V

3) Профильная плоскость T(ABCD)||W

Если фигура || пл-ти проекций, то она проецируется в Н.В. Проекции фигуры на 2 другие пл-ти проекций || осям, определяющую данную пл-ть

Если фигура перпендикулярна пл-ти проекций, то их проекция проецируется в линию и проецируется в НВ. Углы наклона фигуры к двум другим пл-ям проекции проецируется в НВ