1.1 Определение среднего значения полученного результата

Вычисление среднего арифметического представленного массива значений производят по формуле: ;

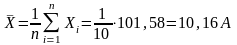где: Х₁, Х₂, X₃, ... X_i, означают n результатов определений какой-либо величины, в нашем примере n=10; Х₁=10,07; Х₂=10,08; Х₃=10,10; X₄=10,12, Х₅=10,13; Х₆=10,15; Х₇=10,16; Х₈=10,17; Х₉=10,20; Х₁₀=10,40 А; 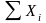=101,58.

1.2 Определение ско данной совокупности (s)

СКО результата измерений (стандартное отклонение) вычисляется по формул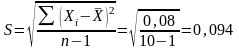е: ; где:

Хi
10,07	10,16	-0,09	0,0081
10,08		-0,08	0,0064
10,10		-0,06	0,0036
10,12		-0,04	0,0016
10,13		-0,03	0,0009
10,15		0,01	0,0001
10,16		0	0
10,17		0,01	0,0001
10,20		0,04	0 0016
10,40		0,24	0,0576
У			0,08

1.3 Вычисление коэффициента вариации (V)

Применяя любой вид статистических показателей, полезно знать, каковы предельные возможности данного показателя для изучаемой системы и каково отношение фактически наблюдаемых значений к предельно возможным. Очевидно, что минимально возможное значение показателя вариации достигается при строго равномерном распределении объемного признака между всеми единицами совокупности. В таком предельном (теоретическом) распределении вариация отсутствует и все её показатели равны нулю. Коэффициент вариации, в частности, характеризует степень отклонения результатов от среднего значения: .

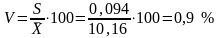Его используют в тех случаях, когда необходимо сравнить степень изменчивости нескольких выборок, имеющих различные усредненные показатели или различные единицы измерения. Если V меньше 20 %, то выборку считают однородной, а среднюю надежной. Если V больше 20 %, то выборка не однородна и средняя не надежна.

1.4 Определение ско погрешности среднего значения ( )

Многократное измерение одной и той же величины постоянного размера позволяет обеспечить требуемую точность. Поскольку ширина доверительного интервала зависит от количества экспериментальных данных, то увеличивая количество измерений одной и той же величины, можно добиться увеличения точности измерений. При этом средняя ошибка средней (стандартная ошибка) вычисляется по формуле: .

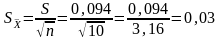Эта формула говорит о том, что, например, при 4-х опытах погрешность измерений уменьшится в 2 раза, при 16 – в 4 раза. Для того, чтобы уменьшить среднюю ошибку выборки в п раз необходимо провести 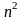определений.