21.Теорема Штейнера-Гюйгенса.

Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции   тела относительно произвольной оси равен сумме момента инерции этого тела   относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела   на квадрат расстояния   между осями:

где

 — известный момент инерции относительно оси, проходящей через центр масс тела,

 — искомый момент инерции относительно параллельной оси,

 — масса тела,

 — расстояние между указанными осями.

22.Момент силы относительно оси вращения. Момент импульса, уравнение моментов.

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

23.Работа силы. Потенциальные силы и их работа.

Работа силы (сил) над одной точкой

• Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения^[3]:

Здесь точкой обозначено скалярное произведение^[4],   — вектор перемещения; подразумевается, что действующая сила   постоянна в течение всего того времени, за которое вычисляется работа.

Если сила не постоянна, то в этом случае она вычисляется как интеграл^[5]:

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений   если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[6], интеграл определяется^[7] следующим образом:

,

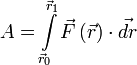где   и   — радиус-векторы начального и конечного положения тела соответственно.

• Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.

Работа силы (сил) над системой или неточечным телом

Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой).

Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

• Эти определения могут быть использованы как для конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.