20. Испытания грунтов в приборах трехосного сжатия.

Сложное напряженное состояние с помощью компрессионных испытаний оценить нельзя. Большую определенность дают трехосные испытания в стабилометрах. Испытание грунта в приборе трехосного сжатия ближе отвечает его работе в природных условиях и даёт наиболее надёжные результаты в определении его прочностных и деформационных свойств.

Т рехосному напряженному состоянию грунт подвергается в стабилометре.

В приборе грунт находится в условиях объёмного напряженного состояния. σ 1 σ 1 σ σ σ 2 Р2 σ 2 σ σ σ 1

Сложное напряженное состояние с помощью компрессионных испытаний оценить нельзя. Большую определенность дают трехосные испытания в стабилометрах. Особенностью трехосных испытаний в стабилометрах является равномерное сжатие образца. Для наблюдениея за деформировнием образца стенки камеры обычно изготавливаются из прозрачного материала. Оценка сжимаемости грунтов в приборах трехосного сжатия производится по объемной деформации грунта

где - изменение объема образца.

В стабилометрах изменение объема образца определяется по объему жидкости, поступающей в камеру прибора или входящей из нее.

21. Определение напряжения в грунте от действия вертикальной сосредоточенной силы.

Рассм. действие вертик. соредоточенной силы N , приложенной в точке О к горизонтальной плоскости , являющейся поверхностью линейно-деформируемого полупространства , простирающегося в бесконечность ниже этой плоскости. От действия силы N во всех точках полупространства возникает сложное напряженное состояние.

Пусть положение точки М1 определяется полярными координатами R и β системы координат с началом в точке приложения силы N. Под действием силы N точка М1 переместиться в направлении радиуса R на величину s1. Чем дальше от точки О будет расположена точка М1 , тем меньше будет ее перемещение ; при R=бесконечности перемещение точки М1будет =0.Следовательно S1 можно принять обратно пропорциональным R. В то же время при одном и том же значении R для различных величин угла β перемещения точек будут неодинаковы. Наибольшее перемещение получит точка , расположенная на оси z , т.е. при β=0. С увеличением угла β перемещения по направлению радиуса R уменьшаются , и в случае β=90 град. При малых деформациях будут =0.В связи с этим можно принять , что перемещение точки М1 по направлению радиуса , кроме зоны около точки приложения силы N, будет

S1=(ά1/R )cosβ, где

ά1-коэфф. пропорциональности.

Эта зависимость удовлетворяет граничным условиям. Рассм. теперь точку М2 на продолжении радиуса R. Пусть точка М2 находиться на расстоянии dR от точки М1.Руководствуясь записанным выражением , найдем перемещение точки М2 по направлению радиуса R:

S2=[ά1/(R+dR)]/cosβ.

Ком случае относительная деформация грунта на отрезке dR составит

Пренебрегая величиной RdR, малой по сравнению с R², и учитывая линейную зависимость между напряжениями и деформациями, найдем выражение для напряжений сжатия, действующих на площадки , перпендикулярные направлению радиуса R, без учета силы тяжести грунта :

, где ά2-коэфф. пропорциональности между напряжениями и деформациями .

Учитывая, что R²=r²+z² ,будем иметь

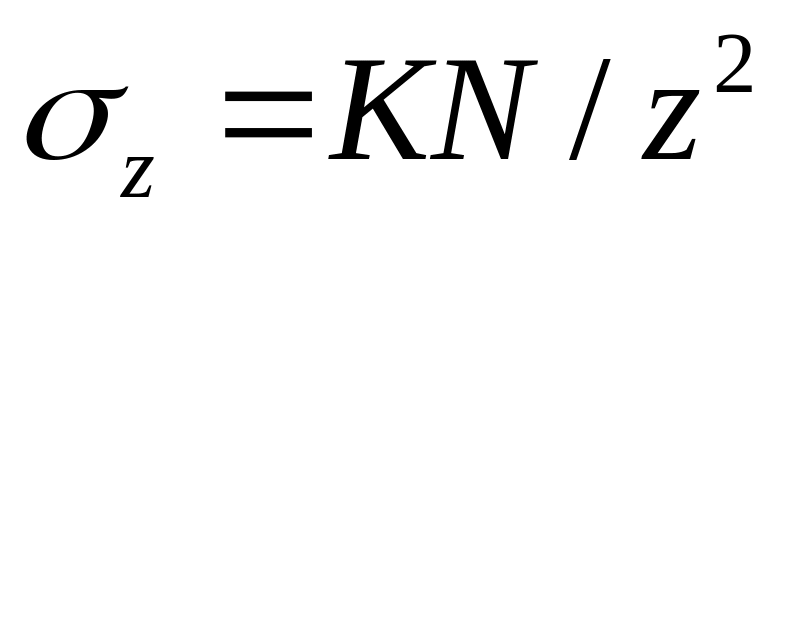, где

Аналогично могут быть найдены остальные компоненты напряжения в точке М1.Подставляя в последнюю формулу значение коэфф. К найденного по таблице определяют вертикальное сжимающее напряжение σz, развивающееся в грунтах при действии сосредоточенной стлы.