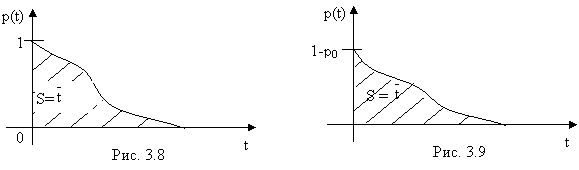3.1. Надёжность элемента. Плотность распределения времени безотказной работы. Среднее время безотказной работы

 

Оценка надежности системы и элементов требует введения количественных характеристик. Рассмот­рим здесь некоторые из этих характеристик. Для краткости будем определять их применительно к "элементу"; однако те же определения будут относиться и к "системе".

Надежностью элемента (в узком смысле слова) называется вероятность того, что данный эле­мент в данных условиях будет работать безотказно в течение времени t. Эту вероятность мы будем обозначать р(t). Функция р(t) называется иногда законом надежности.

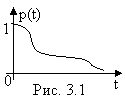
Естественно, с увеличением времени функция р(t) убывает (рис 3.1) При t=0 естественно предполо­жить р(t)=1.

Ненадежностью элемента называется вероятность q(t) того, что элемент откажет (выйдет из строя) в течение времени t. Очевидно, q(t)=1-p(t).

Рассмотрим время T безотказной работы элемента как случайную величину. Функция распределения F(t) этой случайной величины определяется как

F(t)=P(T<t).                                                                                        (3.1)

Очевидно, F(t) - вероятность того, что за время t элемент откажет, - представляет собой не что иное, как ненадежность элемента:  F(t)=q(t), - а его надежность дополняет F(t) до единицы:

p(t)=1-F(t).                                                                                           (3.2)

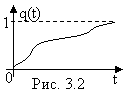
Таким образом, ненадежность q(t) обладает свойствами функции распределения неотрицательной случайной величины. Она равна нулю при t=0, не убывает при возрастании t и стремится к единице при t  (рис. 3.2).

На практике обычно вместо функции распределения F(t) пользуются ее производной — плотностью распределения или плотностью вероятности:

   f(t)=F'(t)=q'(t).                                                                                                 (3.3)

График плотности f(t) показан на рис. 3.3. Площадь, ограниченная кривой f(t), равна единице.

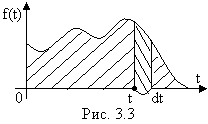
Величина f(t)dt — элемент вероятности — истолковывается как вероятность того, что время T примет значение, лежащее в пределах элементарного участка (t, t+dt).

В литературе надежность функции f(t) часто называют "плотностью отказов". Во избежание недора­зумений, связанных с нечеткой терминологией, мы будем называть f(t) более точно: плотностью рас­пределения времени безотказной работы.

Плотность f(t) может быть приближенно определена из опыта, для чего ставится следующий экспе­римент: наблюдается работа большого числа N однородных элементов; каждый из них работает до мо­мента отказа. Время, в течение которого работал элемент, регистрируется. Полученные значения вре­мени:

t₁, t_{2, ….,} t_N

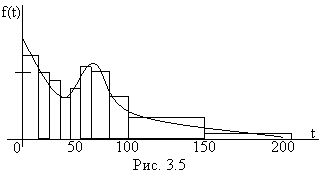
обрабатываются обычными методами математической статистики: строится гистограмма (рис. 3.4) и выравнивается с помощью какой-нибудь плавной кривой, обладающей свойствами плотности.

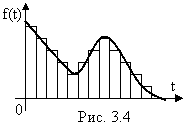
Ордината гистограммы на каждом элементарном участке времени t представляет собой не что иное, как среднее число отказов за единицу времени, приходящееся на один испытанный элемент. Тот же смысл можно приписать и функции f(t). Приближенно плотность f(t) определяется по формуле

,                                                               (3.4)

где m(t, t+t) — число элементов, оказавших на участке времени от t до t+t (время отсчитывается от момента включения); N — общее число элементов, t — длина элементарного участка времени.

Пример. Было испытано N=1000 ламп на длительность безотказной работы. Результаты испытаний приведены в табл. 3.1.

                                                                                                                                         Таблица 3.1

Длительность работы в часах           (от - до)	0-10	10-20	20-30	30-40	40-50	50-60	60-80	80-100	100-150	150-200
Число ламп   m(t, t+t)	151	102	77	61	79	120	200	69	91	50

Найти приближенно плотность f(t) для каждого участка времени, построить гистограмму и выров­нять (от руки) плавной кривой.

Решение. На первом участке (0-10 час) имеем:   ,

на втором  ,

и т.д. Значения плотности f(t) приведены в табл. 3.2.

                                                                                                                                             Таблица 3.2

Длительность работы в часах (от - до)	0-10	10-20	20-30	30-40	40-50	50-60	60-80	80-100	100-150	150-200
Плотность f(t)	0,0151	0,0102	0,0077	0,0061	0,0079	0,012	0,0100	0,0035	0,0017	0,0010

Гистограмма и выравнивающая кривая приведены на рис. 3.5.

Отметим, что плотность f(t), изображенная на рис. 3.5, имеет максимум при t=0, т.е. максимальная частота отказов приходится на начальный период работы элемента. Такой характер кривой f(t) нередко наблюдается на практике, особенно при работе с электро- и радиодеталями, т.к. они часто имеют тен­денцию отказывать немедленно или вскоре после включения. Иногда это повышение плотности в точке t=0 сказывается настолько резко, что заметную долю элементов можно считать отказавшим точно в момент включения. При этом время безотказной работы Т превращается из непрерывной в смешанную случайную величину, у которой одно значение (t=0) обладает отличной от нуля вероятностью p₀, а для других существует только какая-то плотность распределения. Функция распределения такой случайной величины показана на рис. 3.6 – в точке t=0 она имеет скачок, равный р₀, а при t>0 – непрерывна.

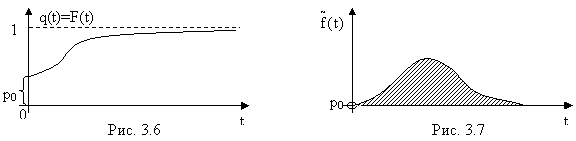
Дифференцируя функцию F(t) при t>0, получим кривую “плотности”  (рис. 3.7). Она характерна тем, что ограничивает площадь, равную уже не единице, а 1-р₀. При обработке экспериментальных дан­ных в таком случае отбирают в отдельную группу элементы, отказавшие при включении, и отношение их числа m₀ к общему числу N испытанных элементов считают за приближенное значение р₀:

,

а для остальных данных строится обычная гистограмма (при этом частоты находятся делением числа наблюдений в разряде на общее число наблюдений N).

В качестве характеристики надежности элемента часто применяют среднее время безотказной ра­боты, т.е. математическое ожидание величины Т:

.

В случае, если величина Т непрерывна (т.е. её функция распределения F(t) не имеет скачка при t=0)

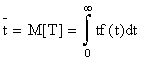.                                                 (3.5)

В случае, когда Т – смешанная случайная величина, и отдельное значение t=0 имеет вероятность р₀,

.                                                               

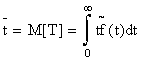Величина  может быть выражена не через плотность распределения f(t), а непосредственно через на­дежность p(t). Действительно,

                                                      .

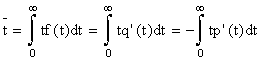Интегрируя по частям, имеем:             .                                      

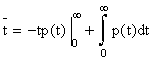Первый член в правой части этого выражения равен нулю, так как для случайной величины T, у ко­торой существует математическое ожидание, разность 1-F(t)=p(t) при t должна убывать быстрее, чем растет t. Поэтому

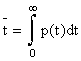                                                      .                                                          (3.6)

Эта формула имеет простую геометрическую интерпретацию: среднее время безотказной работы элемента равно полной площади S, ограниченной кривой надежности и осями координат (рис. 3.8).

Очевидно, в случае, когда T — смешанная случайная величина (значение t=0 имеет вероятность р₀), это правило остается в силе; вся разница в том, что кривая р(t) будет начинаться не от 1, а от 1-р₀ (рис. 3.9).