5.3. Геометрическое распределение

 

Говорят, что случайная величина Х имеет геометрическое распределение, если её возможные значе­ния 0,1,2, …, m, …, а вероятности этих значений:

                   P_m=q^mp,                                                                                                                  (5.3.1)

где 0<p<1; q=1-p; m=0,1,2,…

Вероятности P_m для последовательных значений m образуют геометрическую прогрессию с первым членом р и знаменателем q (отсюда и название «геометрическое распределение»):

                   P₀=P{X=0}=p;  P₁=P{X=1}=qp; …,   P_m=P{X=m}=q^mp.                                                      (5.3.2)

На практике геометрическое распределение появляется в следующих условиях. Пусть производится ряд независимых опытов, с целью получения какого-то результата («успеха») А; при каждой попытке (опыте) «успех» достигается с вероятностью р. Случайная величина Х – число «безуспешных» попыток (до первой попытки, в которой появляется результат А). Нетрудно убедиться, что случайная величина Х имеет геометрическое распределение (5.3.2). Действительно,

                   P{X=0}=P{первая же попытка успешна}=p,

                   P{X=1}=P{первая попытка безуспешна, вторая успешна}=qp,

……

P{X=m}=P{первые m попыток безуспешные, (m+1)-я успешна}=q^mp.

……

Ряд распределения случайной величины Х имеет вид:  .

Первые четыре ординаты  геометрического распределения для р=0,4; q=0,6 показаны на рисунке 5.3.1.

 

 

 

 

 

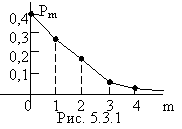
Найдем числовые характеристики случайной величины Х, распределенной по геометрическому за­кону. Для этого запишем её производящую функцию:

                   .

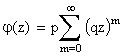Суммируя бесконечно убывающую геометрическую прогрессию со знаменателем qz<1, получим

                   (z)=p(1-qz)^-1.                                                                                    (5.3.3)

Дифференцируя выражение (5.3.3) по z, найдем:

                   ’(z)=pq(1-qz)^-2.                                                                                   (5.3.4)

Откуда находим математическое ожидание:     m_x=’(1)=pq(1-q)^-2.

Сокращая на p=1-q, находим:

                   m_x=q/p.                                                                                           (5.3.5)

Дифференцируя ещё раз (5.3.4), имеем

                   ”(z)=2pq²(1-qz)^-3;

                   ”(1)=2pq²(1-q)^-3=2q²/p².

Отсюда находим второй начальный момент случайной величины Х:

                   ₂=”(1)+m_x=2q²/p²+q/p=q(2q+p)/p².

Но 2q+p=q+p+q=1+q (так как p+q=1); отсюда

                   ₂= q(1+q)/p².                                                                                       (5.3.6)

Вычитая из (5.3.6) , находим дисперсию случайной величины Х

                   D_x=q/p²                                                                                                                                    (5.3.7)

и, наконец, среднее квадратическое отклонение

                   .                                                                         (5.3.8)

На практике чаще приходится рассматривать не случайную величину Х, имеющую геометрическое распределение, а другую случайную величину:

                   Y=X+1                                                                                                                                    (5.3.9)

(число попыток до первого «успеха», включая удавшуюся).

Ряд распределения случайной величины Y имеет вид:         .

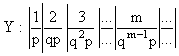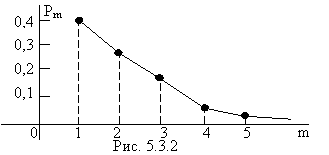
Будем называть такое распределение «геометрическим, сдвинутым на единицу» или «геометриче­ским +1». Многоугольник распределения случайной величины Y при р=0,4 имеет тот же вид, что и на рис. 5.3.1, но сдвинут вправо на одну единицу (рис.5.3.2).

Найдем математическое ожидание и дисперсию случайной величины Х. Пользуясь свойствами чи­словых характеристик, приведенными ранее, получим

                   m_y=M[X+1]=m_x+1=q/p+1=1/p                                                                                    (5.3.10)

                   D_y=D[X+1]=D_x=q/p²,                                                                                                  (5.3.11)

                   .                                                          (5.3.12)

Пример 1. При  каждом цикле обзора радиолокатора объект (независимо от других циклов) обнару­живается с вероятностью р=0,2. Найти математическое ожидание и дисперсию числа Х циклов обзора, которое придется произвести без обнаружения объекта и числа Y циклов обзора, которое придется про­извести вплоть до обнаружения объекта (включая тот, при котором объект будет обнаружен). Найти ма­тематическое ожидание, дисперсию и среднее квадратическое отклонение каждой из случайных вели­чин Х, Y. Пользуясь правилом трех сигма, найти максимальное практическое возможное число циклов, за которое объект ещё не будет обнаружен. Найти вероятность того, что фактическое число «безуспеш­ных» циклов превзойдет его математическое ожидание больше, чем на 3.

Решение. Случайная величина Х имеет геометрическое распределение с параметром р=0,2; по фор­мулам (5.3.5), (5.3.7) и (5.3.8) имеем:

                   m_x=(1-0,2)/0,2=4;        D_x=0,8/0,04=20;          _x= ;

случайная величина Y имеет «геометрическое +1» распределение; её математическое ожидание m_y=4+1=5; её дисперсия такова же, как дисперсия случайной величины Х:

                        D_y=20;             _y4,46.

Найдем      P{X>m_x+3}=P{X>4+13}=1-P{X17}=1-p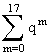 =1-(p-pq¹⁸)/(1-q)=q¹⁸=0,8¹⁸0,0180144.

Таким образом, вероятность того, что случайная величина Х превзойдет свое математическое ожида­ние больше, чем на 3, довольно мала (меньше 2%; отклонения в меньшую сторону не рассматриваем, так как они приводят к отрицательным значениям Х, что вообще невозможно).

Пример 2. В нашем распоряжении имеется n лампочек; каждая из них с вероятностью p имеет де­фект. Лампочка ввинчивается в патрон и в сеть включается ток; при включении тока дефектная лам­почка сразу же перегорает и заменяется другой. Рассматривается случайная величина Z – число лампо­чек, которое будет испробовано. Построить ряд распределения случайной величины Z и найти её мате­матическое ожидание.

Решение. Распределение случайной величины Z для всех значений m<n есть «геометрическое +1» распределение с параметром q=1-p. Найдем P{Z=n}. Это есть вероятность того, что будут испробованы все n лампочек, а значит, первые n-1 лампочек окажутся дефектными. Следовательно, P{Z=n}=p^n-1.

Ряд распределения случайной величины Z имеет вид: 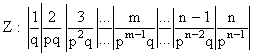   , где q=1-р.

Производящая функция случайной величины Z равна

                   .

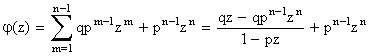Её производная:    .

Полагая в ней z=1, получим

                   .