1.6. Стрингерный отсек

Стрингерный отсек равноустойчив для обшивки и стрингеров, а на диаграмме, изображенной на рис. 6, соответствует точке С. Обшивка такого отсека подкрепляется продольным силовым набором и поперечным – шпангоутами. Схема стрингерного отсека приведена на рис. 7.

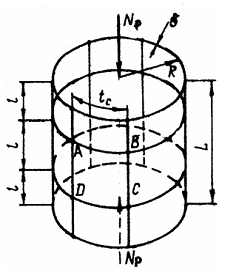
Рис. 7. Стрингерный отсек

Под действием осевой сжимающей силы N_p в поперечных сечениях отсека возникают меридиональные напряжения

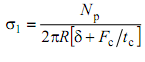, (1.19)

где t_c - шаг, а F_c – площадь поперечного сечения стрингера. Весь отсек работает на общую устойчивость, а отдельные его элементы – на местную. Критические напряжения общей потери устойчивости конструктивно-анизотропной оболочки определяются по формуле (1.9), но теперь , где F_шп – площадь шпангоута; J_c – момент инерции стрингера; – цилиндрическая жесткость обшивки.

В этом случае получаем при μ = 0,3 теоретическую формулу

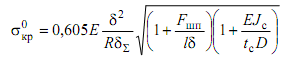, (1.20)

из которой находим выражение для N_кр, заменив также теоретический коэффициент 0,605 на k = 0,4…0,5 для стрингерных оболочек:

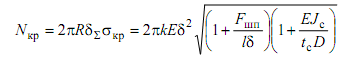, (1.21)

где δ_Σ – эквивалентная толщина отсека, с учетом площади стрингеров δ_Σ= δ +F_с/ t_с.

Устойчивость может также потерять участок стрингера длиной l между соседними шпангоутами. Критические напряжения определим по формуле Эйлера6

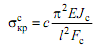, (1.22)

где с=2 – коэффициент, учитывающий способ закрепления концов стрингера.

Местная потеря устойчивости может также наблюдаться для участка обшивки ABCD (рис. 7), а критическое напряжение для шарнирно закрепленной пластинки

. (1.23)

Для определения конструктивных размеров отсека предположим, что отсек и все его элементы теряют устойчивость при одинаковых критических напряжениях σ_кр, которые известны. . Тогда, воспользовавшись условием равноустойчивости обшивки и стрингеров из (1.18), получаем толщину обшивки:

Расстояние между стрингерами находим из (1.23): . Так как σ₁ = σ_кр , то из (1.19) находим площадь стрингера . Расстояние между шпангоутами находится из (1.22): .

Задаемся формой сечения стрингера и находим коэффициент k_c в выражении, связывающем момент инерции сечения стрингера J_c и его площадь . Тогда . Теперь площадь шпангоута находится из условия общей устойчивости отсека (1.21):

Более точное значение σ_кр можно получить из условия минимума массы отсека: . В этом случае проводится проектировочный расчет массы отсека при различных значениях σ_кр и строится график зависимости m= m(σ_кр).

Точка минимума на графике соответствует значению σ_кр , которое необходимо использовать при определении размеров отсека. Отсек минимальной массы не обязательно получается при σ_кр , равном пределу текучести. В дальнейшем размеры элементов отсека уточняются на стадии конструкторского проектирования, поэтому он не обязательно будет равноустойчивым и иметь ту же массу, что и на стадии проектировочного расчета.

1.7. Лонжеронный отсек

В лонжеронном отсеке (рис. 8) толщина обшивки δ выбирается из технологических соображений. Обшивка в лонжеронном отсеке теряет устойчивость раньше, чем лонжероны. Вместе с лонжеронами работает только участок присоединенной обшивки, примыкающей к ним.

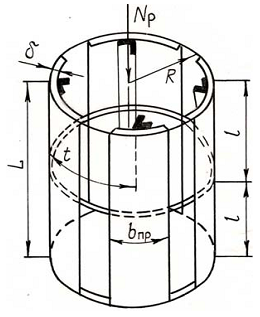
Рис. 8. Схема нагружения лонжеронного отсека

Тогда напряжения в отсеке, сжатом осевой силой Np, определяются по формуле

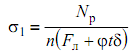, (1.24)

где n, F_л – количество лонжеронов и площадь; φ = b_пр/ t – редукционный коэффициент; b_пр , t – ширина присоединенной обшивки и расстояние между лонжеронами.

Если воспользоваться формулой Кармана для определения ширины присоединенной обшивки, то

, (1.25)

где σ^л_кр – критические напряжения лонжерона. Определив расстояние между лонжеронами t= 2π R / n , получим следующее выражение для редукционного коэффициента:

.

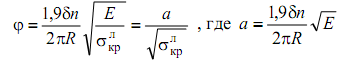Расчетная схема отсека показана на рис. 46, где изображена только работающая часть обшивки. Формула для критических напряжений общей устойчивости лонжеронного отсека аналогична (1.20) для стрингерного, за исключением того, что в выражении для осевой жесткости необходимо пренебречь цилиндрической жесткостью обшивки D, а под

моментом инерции продольного элемента понимать момент инерции сложного сечения, состоящего из лонжерона и присоединенной обшивки, который будем обозначать далее J_Σ. Теперь вместо (7.21) имеем

,

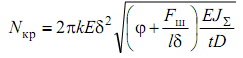где k = (0,4…0,5) – коэффициент.

Критические напряжения потери устойчивости лонжерона с присоединенной обшивкой как стержня, сжатого осевой силой:

, (1.26)

где – радиус инерции сечения, состоящего из лонжерона и присоединенной обшивки; – суммарная площадь этого сечения; c=2 – коэффициент, учитывающий закрепление краев лонжерона. Считаем отсек равноустойчивым, а σ_кр – критические напряжения, δ – толщина обшивки, n – количество лонжеронов – известными. Тогда площадь лонжерона можно найти из (1.24), приняв σ₁ = σ_кр :

.

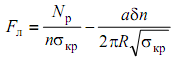Из (1.26) расстояние между шпангоутами

,

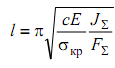где площадь F_Σ известна, а момент инерции суммарного сечения можно определить, если задаться формой поперечного сечения лонжерона. Форму профиля можно подобрать исходя из полученной площади сечения лонжерона и условий местной устойчивости пластинок профиля. Кроме площади будем также считать известной ширину полки со свободным краем, определяемую технологическими соображениями, или толщину профиля h, по отношению к толщине обшивки, считая ее в несколько раз большей δ , для того чтобы обшивка при потере устойчивости не повлекла за собой полки лонжерона, скрепленные с ней.

Для определения формы профиля введем понятие базовой пластинки, один размер которой задан, а второй определим из условия местной устойчивости пластинки со свободным краем, которое запишется так: . Беря знак равенства, находим , где h – толщина профиля, совпадающая с толщиной базовой пластинки; b – ширина базовой пластинки. Теперь определим количество базовых пластинок, которые имеют суммарную площадь, равную площади лонжерона F_л: , где квадратными скобками обозначена целая часть результата деления выражения, записанного в скобках. Далее выбираем форму профиля лонжерона в зависимости от k_пл: k_пл = 1 – при заданной нагрузке лонжеронный отсек на разрушающие напряжения не может быть спроектирован;

k_пл = 2 – уголковый профиль;

k_пл = 3…4 – зетаобразный профиль;

k_пл = >4 – корытообразный профиль.

Максимальное количество k_пл, обеспечивающее местную устойчивость полок и стенок лонжерона не должно превышать заданного значения (k_пл ) _max.

Определим теперь геометрические характеристики суммарного сечения в зависимости от формы профиля. Уголковый профиль (k_пл =2) (рис. 47,а). Площадь лонжерона .