Задание n 6 Тема: Динамика вращательного движения

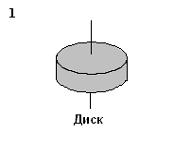
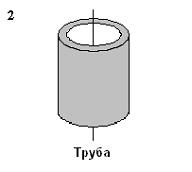
Рассматриваются три тела: диск, тонкостенный цилиндр (труба) и шар; причем массы m и радиусы R оснований диска и трубы и радиус шара одинаковы. Для моментов инерции рассматриваемых тел относительно указанных осей верным является соотношение …

Решение: Момент инерции сплошного однородного кругового цилиндра (диска) массы m и радиуса R относительно его оси вычисляется по формуле ; момент инерции тонкостенного кругового цилиндра (трубы) массы m и радиуса R относительно его оси – по формуле ; момент инерции шара массы m и радиуса R относительно оси, проходящей через его центр, – по формуле . В данном случае для шара ось вращения не проходит через его центр. Используя теорему Штейнера, можно найти момент инерции шара относительно указанной оси: . Поэтому правильным для моментов инерции рассматриваемых тел относительно указанных осей является соотношение .

Задание n 7 Тема: Волны. Уравнение волны

Продольными волнами являются …

			звуковые волны в органных трубах
			световые волны в вакууме
			волны, распространяющиеся вдоль струн музыкальных инструментов
			волны на поверхности воды

Решение: При распространении звуковой волны частицы воздуха в трубе органа колеблются в направлении распространения волны. Следовательно, эти волны относятся к продольным. Упругими поперечными волнами являются волны, распространяющиеся вдоль струн музыкальных инструментов, так как в струне возникает деформация сдвига, и частички струны колеблются в направлении, перпендикулярном направлению распространения волны вдоль струны. Радиоволны и световые волны – электромагнитные волны, следовательно, также поперечные. В электромагнитной волне векторы напряженностей электрического и магнитного полей колеблются в плоскостях, перпендикулярных направлению распространения волны.

 ЗАДАНИЕ N 8 Тема: Свободные и вынужденные колебания

Материальная точка совершает гармонические колебания по закону . Максимальное значение скорости точки (в м/с) равно …

  ЗАДАНИЕ N 9 Тема: Энергия волны. Перенос энергии волной

Если увеличить в 3 раза амплитуду волны, то плотность потока энергии увеличится в _______ раз(-а).

			9
			1,5
			3
			4,5

Решение: Плотность потока энергии, то есть количество энергии, переносимой волной за единицу времени через единицу площади площадки, расположенной перпендикулярно направлению переноса энергии, равна: , где – объемная плотность энергии, – скорость переноса энергии волной (для синусоидальной волны эта скорость равна фазовой скорости). Среднее значение объемной плотности энергии равно: , где – амплитуда волны,  – частота. Следовательно, плотность потока энергии увеличится в 9 раз.