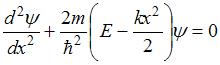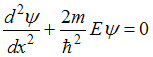- •Задание n 4 Тема: Свободные и вынужденные колебания
- •Задание n 5 Тема: Тепловое излучение. Фотоэффект
- •Задание n 9 Тема: Явление электромагнитной индукции
- •Задание n 10 Тема: Уравнения Максвелла
- •Задание n 11 Тема: Магнитостатика
- •Задание n 12 Тема: Законы постоянного тока
- •Задание n 13 Тема: Электростатическое поле в вакууме
- •Задание n 14 Тема: Электрические и магнитные свойства вещества
- •Задание n 19 Тема: Кинематика поступательного и вращательного движения
- •Задание n 20 Тема: Работа. Энергия
- •Задание n 21 Тема: Уравнение Шредингера (конкретные ситуации)
- •Задание n 22 Тема: Уравнения Шредингера (общие свойства)
- •Задание n 23 Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Задание n 24 Тема: Спектр атома водорода. Правило отбора
- •Задание n 1 Тема: Динамика поступательного движения
- •Задание n 4 Тема: Кинематика поступательного и вращательного движения
- •Задание n 5 Тема: Элементы специальной теории относительности
- •Задание n 6 Тема: Динамика вращательного движения
- •Задание n 7 Тема: Волны. Уравнение волны
- •Задание n 10 Тема: Сложение гармонических колебаний
- •Задание n 11 Тема: Явление электромагнитной индукции
- •Задание n 12 Тема: Электростатическое поле в вакууме
- •Задание n 13 Тема: Законы постоянного тока
- •Задание n 14 Тема: Магнитостатика
- •Задание n 15 Тема: Уравнения Максвелла
- •Задание n 16 Тема: Электрические и магнитные свойства вещества
- •Задание n 22 Тема: Первое начало термодинамики. Работа при изопроцессах
- •Задание n 25 Тема: Интерференция и дифракция света
- •Задание n 26 Тема: Тепловое излучение. Фотоэффект
- •Задание n 27 Тема: Эффект Комптона. Световое давление
- •Задание n 28 Тема: Поляризация и дисперсия света
Задание n 19 Тема: Кинематика поступательного и вращательного движения
Точка
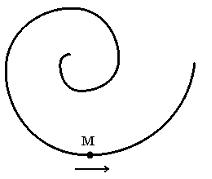
М движется по спирали с равномерно
убывающей скоростью в направлении,
указанном стрелкой. При этом величина
тангенциального ускорения точки …
|
|
|
не изменяется |
|
|
|
увеличивается |
|
|
|
уменьшается |
|
|
|
равна нулю |
Решение:
Величина
тангенциального ускорения определяется
соотношением
![]() .
Так как по условию скорость убывает
равномерно, величина тангенциального
ускорения остается постоянной.
.
Так как по условию скорость убывает
равномерно, величина тангенциального
ускорения остается постоянной.
Задание n 20 Тема: Работа. Энергия
Потенциальная
энергия частицы задается функцией
![]() .
.
![]() –
компонента (в Н) вектора силы,
действующей на частицу в точке А (1, 2, 3),
равна …
(Функция
–
компонента (в Н) вектора силы,
действующей на частицу в точке А (1, 2, 3),
равна …
(Функция
![]() и
координаты точки А и заданы в единицах
СИ.)
и
координаты точки А и заданы в единицах
СИ.)
|
|
|
– 4 |
|
|
|
4 |
|
|
|
12 |
|
|
|
– 12 |
Решение:
Связь
между потенциальной энергией частицы
и соответствующей ей потенциальной
силой имеет вид
![]() ,
или
,
или
![]() ,
,
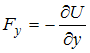 ,
,
![]() .
Таким образом,
.
Таким образом,
![]()
Задание n 21 Тема: Уравнение Шредингера (конкретные ситуации)
Электрон
находится в одномерной прямоугольной
потенциальной яме с бесконечно высокими
стенками в состоянии с квантовым числом
n = 4. Если
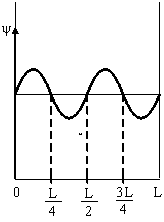
![]() -функция
электрона в этом состоянии имеет вид,
указанный на рисунке, то вероятность
обнаружить электрон в интервале от
-функция
электрона в этом состоянии имеет вид,
указанный на рисунке, то вероятность
обнаружить электрон в интервале от
![]() до
до
![]() равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Вероятность
обнаружить микрочастицу в интервале
(a,
b)
для состояния, характеризуемого
определенной
-функцией,
равна
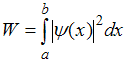 .
Из графика зависимости
.
Из графика зависимости
![]() от
х
эта вероятность находится как отношение
площади под кривой
в
интервале (a,
b)
к площади под кривой во всем интервале
существования
от
х
эта вероятность находится как отношение
площади под кривой
в
интервале (a,
b)
к площади под кривой во всем интервале
существования
![]() ,
то есть в интервале (0,
L).
Очевидно, что график зависимости
от
х
схематически можно представить следующим
образом:
,
то есть в интервале (0,
L).
Очевидно, что график зависимости
от
х
схематически можно представить следующим
образом:
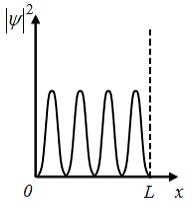 Тогда
вероятность обнаружить электрон в
интервале от
до
равна
Тогда
вероятность обнаружить электрон в
интервале от
до
равна
![]()
Задание n 22 Тема: Уравнения Шредингера (общие свойства)
Стационарное
уравнение Шредингера в общем случае
имеет вид
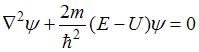 ,
где
,
где
![]() потенциальная
энергия микрочастицы. Движение частицы
вдоль оси ОХ под действием квазиупругой
силы описывает уравнение …
потенциальная
энергия микрочастицы. Движение частицы
вдоль оси ОХ под действием квазиупругой
силы описывает уравнение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
частицы, движущейся вдоль оси ОХ под
действием квазиупругой силы, то есть
силы, пропорциональной отклонению х
частицы от положения равновесия,
выражение для потенциальной энергии
имеет вид
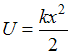 .
Кроме того, для одномерного случая
.
Кроме того, для одномерного случая
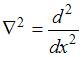 .
Поэтому движение частицы вдоль оси ОХ
под действием квазиупругой силы описывает
уравнение
.
.
Поэтому движение частицы вдоль оси ОХ
под действием квазиупругой силы описывает
уравнение
.