Раздел 2. «гидрология»

Задача № 2.1 Задание.

По результатам промера глубины в расчетном поперечнике реки и измерения продольного уклона свободной поверхности определить расход воды в реке.

Подсчитать расходы Q при различных уровнях воды Н и построить кривую связи уровней воды Н с расходами Q, т. е.Q=f(Н).

Исходные данные.

Расстояния от урезов воды правого и левого берега до ближайшей промерной вертикали – 2 м, число промерных вертикалей – 14, расстояния между промерными вертикалями – 2 м.

Условный уровень воды во время замера Z=52 м. Уклон свободной поверхности воды I=0,0004.

Коэффициент шероховатости русла n=0,025

Таблица 2.1

Глубина потока на вертикалях

№ вертикали	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Глубина воды на вертикалях h, м *	0,8	1,5	1,75	2,4	2,45	2,5	2,72	2,58	2,13	1,85	1,45	1,34	0,75	0,68

* Глубина потока на вертикалях определяется как (h+0,1n), где n – последняя цифра шифра.

Методические указания к решению задачи № 2.1

Расход воды Q есть объем воды, протекающей через живое сечение потока в единицу времени.

Определение расхода воды по площади живого сечения и продольному уклону водной поверхности сокращенно называется способом «уклон - площадь». Он основан на применении формулы равномерного движения жидкости (формулы Шези), которая имеет вид

Q C RI v, (1.1)

где - площадь живого сечения потока, м², т.е. сечения нормального к направлению

течения; С - коэффициент Шези, м^0,5/с; I - уклон водной поверхности;

R=ω/χ - гидравлический радиус, м; χ - длина смоченного периметра русла, м (подводного периметра).

Из формулы (1.1) следует, что для определения расхода воды необходимо измерить площадь водного сечения ω, продольный уклон водной поверхности I и вычислить гидравлический радиус R и коэффициент Шези C.

Площадь водного сечения подсчитывают по материалам промерных работ на гидравлическом створе.

Продольный уклон водной поверхности определяется нивелированием уровней воды на концах выбранного участка реки.

Коэффициент Шези С зависит от гидравлического радиуса R и степени шероховатости русла п и может быть вычислен по формуле Н.Н. Павловского при значениях гидравлического радиуса 0,1<R<3.0 м

С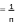 R^y,

(1.2)

где y – переменный показатель степени, зависящий от п и R и определяемый по

ф ормуле y 2,5 n 0,13 0,75 R( n 0,10).(1.3)

В Приложение 2.1 приводятся значения коэффициента Шези С, вычисленные по формуле Павловского при разных значениях R и n= 0,025.

Порядок решения задачи.

В соответствие с установленным вариантом задания по глубинам и расстояниям между промерными вертикалями строят профиль водного сечения. Построение профиля производится на формализованном бланке, приведенном на рис. 2.1.1.

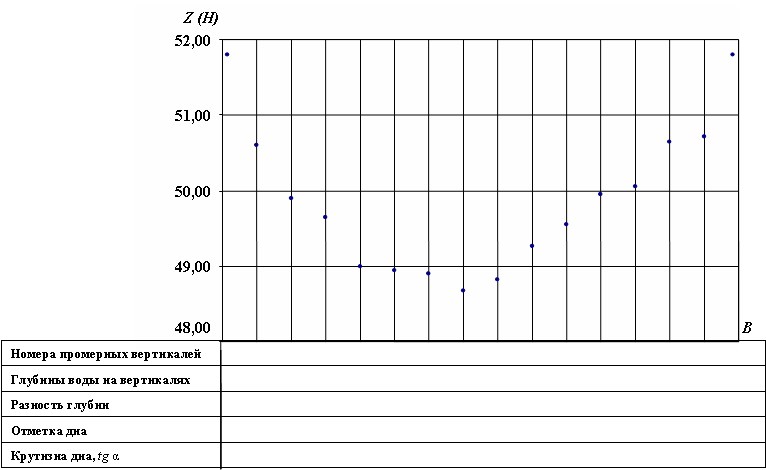
Рис. 2.1.1. Профиль водного сечения

Вертикальный масштаб обычно принимают крупнее горизонтального.

Под профилем выписывают номера промерных вертикалей, глубины воды на вертикалях, разность глубин между соседними вертикалями, отметку дна реки, крутизну дна между промерными вертикалями. Последние значения необходимы для определения площадей живых сечений потока при разных уровнях воды. Поверхность воды обозначается горизонтальной линией с указанием отметки уровня воды. Профиль дна строят, откладывая глубины вниз от расчетного уровня воды. Разность между отметкой поверхности воды и глубиной дает отметку дна реки.

Для профиля вычисляют основные морфометрические характеристики, необходимые для гидрологических и гидравлических расчетов: площадь водного сечения ω; ширину реки В; среднюю глубину h_ср; наибольшую глубину h_наиб.; длину смоченного периметра поперечного сечения русла χ; гидравлический радиус R .

Площадь водного сечения ωможет быть определена суммированием площадей, ограниченных промерными вертикалями, дном и поверхностью воды.

Для прибрежных участков, если h₀=h_n=0, площадь водного сечения ω определяется по формулам:ω₁=h₁в₁/2 и ω_п=h_пв_п/2. (1.4)

Для всех остальных участков площади, ограниченные промежуточными вертикалями, представляют собой трапецию и могут быть вычислены по формулам: 3 в3.

2 2 (1.5)

Общая площадь водного сечения

(1.6)

Здесь h¹,h²,h³,...hⁿ - местные глубины, м; ^{в1,в2,в3,...вn} - расстояние между промежуточными вертикалями, м (сумма этих расстояний между промежуточными вертикалями дает ширину реки В).

Длина смоченного периметра

(1.7)

Наибольшая глубина ^h _наиб выбирается из результата промера глубин.

Гидравлический радиус определяется по формуле

R

С редняя глубина вычисляется отношением

h

^ср B (1.8)

Подставляя все величины в формулу (1.1), получим расход Q, пропускаемый данным сечением реки.

Измерение расходов воды на реках достаточно трудоемкая задача, поэтому их измеряют сравнительно редко. Значительно проще и чаще ведутся наблюдения за уровнем воды. Между расходом воды и уровнем (или глубиной) существует гидравлическая часть.

Обычно она выражается графически в виде графика ^Q=f(h), который называется кривой расхода воды. Имея кривую расхода, можно по установленным уровням Z (или глубине H) определить расходы воды ^Q, не измеряя их.

Кривая расходов ^Q=f(H)строится в прямоугольной системе координат, причем по сои ординат откладывают уровни воды Z (или глубины H), а оси абсцисс - значение измеренных расходов воды ^Q.

В данной задаче расходов произвести определение расходов при уровнях реки в воде 51,8 м; 51,6м; 51,4м и 51,0 м.

П ри каждом новом уровне воды будут изменяться глубины воды на вертикалях, ширина реки и расстояния от уреза воды до ближайшей промерной вертикали. Глубины воды будут уменьшаться на величину понижения уровня H , а расстояние от уреза воды правого и левого берега до ближайшей промерной вертикали следует определить по формуле

hn H вn,

^tg _n (1.9)

г де tg - крутизна дна, определяемая по формуле tg =(h_n+1-h_n)/b

Здесь h – глубина воды на промерной вертикали; b – расстояние между промерными вертикалями.

На основании данных расчетов расходов воды при установленных уровнях воды строят кривую расходов ^Q=f(H).Построение графиков производится на формализованном бланке, приведенном на рис. 2.1.2.

Рис. 2.1.2. Кривая расходов воды Q=f(H)

Задача № 2.2 Задание.

Определить расход воды в реке по скоростям, измеренным гидрометрической вертушкой.

Исходные данные.

Исходные данные представлены в таблице 2.2.1.

Таблице 2.2.1 - Скорость потока на вертикалях

№ вертикали	Расстояние от уреза правого берега, м	Рабочая глубина h, м	Глубина опускания вертушки, в долях рабочей глубины	Скорость в точке U, м/с
I II III IV V	5,0 11,0 15,0 21,0 25,0 30,62	2,10 2,29 2,19 2,23 2,14 0	пов. 0,2 0,6 0,8 дно пов. 0,2 0,6 0,8 дно пов. 0,2 0,6 0,8 дно пов. 0,2 0,6 0,8 дно пов. 0,2 0,6 0,8 дно	0,20 0,20 0,12 0,11 0,08 0,24 0,22 0,21 0,17 0,12 0,25 0,25 0,24 0,20 0,14 0,16 0,16 0,15 0,09 0,08 0,16 0,14 0,12 0,09 0,08

Варианты исходных данных: рабочая глубина (h+ 0,1п) м; скорость в точке (U+0,01n) м/с, где п – последняя цифра шифра.

Методические указания к решению задачи № 2.2

В таблице 2.2.1. представлены скорости течения, измеренные гидрометрической вертушкой. Гидрометрической вертушкой измеряют истинные скорости течения воды и в строго фиксированных точках потока на заранее назначенных вертикалях. Вертикали, на которых измеряется скорости течения, называются скоростными.

Рабочей глубиной на вертикали называется глубина от поверхности воды до дна.

Скорости течения на вертикалях измеряются в пяти точках: у поверхности; на 0,2; 0,6; 0,8 глубины (считают от поверхности) и у дна. Если из-за малости глубины (расстояние между точками должно быть не менее 1,5 диаметра лопастного винта вертушки) не представляется возможным вести измерения во всех точках, то число их сокращается в следующем порядке: остаются точки 0,2; 0,6 и 0,8 глубины; остаются точки 0,2 и 0,8; наконец остается точка 0,6 глубины.

Средняя скорость на скоростной вертикали определяется в зависимости от числа точек измерения по формулам

Uв0,10(Uпов 3U0,2 3U0,6 2U0,8 Uдон)(2.1)

Uв0,25(U0,2 2U0,6 U0,8)(2.2)

U в0,50(U0,20,8)

(2.3)

U вU 6

⁰, (2.4) Порядок решения задачи.

В соответствие с установленным вариантом задания вычисляют средние скорости течения на вертикалях.

П осле вычисления средних скоростей на вертикалях, определяется удельный расход воды на каждой вертикали по формуле ^qhUв, (2.5)

где h – рабочая глубина на вертикали.

После подсчета удельных расходов на вертикалях производится вычисление расхода воды в реке по формуле

Q ,

2 2 (2.6)

г де q¹,q²...qⁿ - удельные расходы воды на вертикалях; ^{в1,в2...вn1}- расстояние между скоростными вертикалями; k – коэффициент для скоростей на приборных вертикалях, принимаемый равным: 0,7 - при пологом береге c h=0 на урезе; 0,8 - при обрывистом береге реки (для условий данной задачи принять k=0,7).

Задача № 2.3 Задание.

Определить максимальный расчетный расход в заданном створе водотока с вероятностью превышения Р=0,33 % на основании многолетних гидрометрических измерений максимальных расходов.

Исходные данные.

Исходные данные, приведенные в табл. 2.3.1,включают значения максимальных годовых расходов воды в реке для каждого условного года наблюдений.

Таблица 2.3.1 - Исходные данные

Условный год	Максимальный расход Qmax, м3/с	Условный год	Максимальный расход Qmax, м3/с
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24	102+n 95+n 89+n 113+n 93+n 110+n 97+n 63+n 96+n 80+n 126+n 107+n 88+n 59+n 116+n 99+n 118+n 79+n 76+n 101+n 92+n 68+n 85+n 103+n	25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47	112+n 84+n 120+n 91+n 94+n 62+n 83+n 100+n 53+n 90+n 129+n 82+n 78+n 72+n 131+n 81+n 47+n 142+n 87+n 155+n 74+n 86+n 136+n
		Примечание: n – две последние цифры учебного шифра.

Методические указания к решению задачи 2.3

Расчетный расход воды является главной гидрологической характеристикой.

Расчетным максимальным расходом воды называют расход, на пропуск которого рассчитывают отверстия мостов. Чем больше расчетный расход, тем больше должно быть отверстие моста или трубы. Увеличение расхода вызывает повышение соответствующего ему уровня воды, а это увеличивает высоту насыпи подходов к мосту или трубе. Следовательно, повышение расчетного расхода приводит к удорожанию всего перехода.

Уменьшение расчетного расхода хотя и приводит к удешевлению перехода, но повышает вероятность повреждения или разрушения перехода водным потоком.

Превышение характеристик потока над расчетными является основной причиной, угрожающей нормальной эксплуатации большинства мостов. Такое превышение может привести к аварийным ситуациям и даже катастрофическим последствиям, вплоть до полного разрушения мостов, насыпей, дорожных труб и т. д.

Надежность работы перехода определяется не только величиной расчетного расхода, но и его повторяемостью. Если более высокие расходы встречаются редко, то можно считать, что переход, рассчитанный на этот расход, будет иметь высокую надежность на пропуск паводков. Если расходы выше расчетного встречаются часто, переход надежным считать нельзя.

Поэтому определение вероятных расходов воды в реке, в частности максимальных, принимаемых для расчета сооружений переходов через водотоки, производится методом математической статистики с учетом ряда наблюдавшихся расходов как нескольких случайных величин.

Определение расчетных гидрологических характеристик при наличии данных гидрометрических наблюдений достаточной продолжительности осуществляется непосредственно по этим данным путем применения аналитических функций распределения ежегодных вероятностей превышения.

Эмпирические кривые распределения ежегодных вероятностей превышения строятся на клетчатках вероятностей.

Основой построения кривой обеспеченности служит ряд эмпирических данных гидрометрических наблюдений за стоком воды, например, расходов воды в реке.Если распределить хронологический ряд максимальных расходов воды Q₁,Q₂,Q₃,…Q_nв убывающем прядке получим статистический ряд.

Если имеется статистический ряд наблюдавшихся расходов с числом лет наблюдений n, то может быть вычислена вероятность появления одного из них с порядковым номером m.

Эмпирическая ежегодная вероятность превышения Р_т гидрологических

характеристик определяется по формуле

Р _m100%,

(3.1)

где Р (%) - обеспеченность каждого ранжированного значения ряда; m – порядковые

номера членов ряда, расположенные в убывающем порядке; n – число лет наблюдений.

Полученные значения обеспеченностиР (%) наносят на график Q=f(P), где на оси ординат находятся величины среднегодовых расходов воды, а на оси абсцисс – вероятность превышения (обеспеченность) Р(%) (рис. 2.3.1).

К полученному семейству точек подбирается аналитическая кривая обеспеченности или проводится сглаженная (усредняющая) эмпирическая кривая обеспеченности. Полученная кривая Q=f(P%) называется эмпирической кривой обеспеченности максимальных расходов воды.

Кривая обеспеченности характеризует распределение расходов воды и показывает, в каком числе случаев, выраженном в процентах, из общего числа случаев, принятых за 100%, будет наблюдаться или превышена (или не превышена) данная величина среднегодового расхода.

При этом термин «вероятность превышения (обеспеченность)», например, Р=1% означает, что превышение расхода вероятно в одном случае из 100, а «вероятность превышения (обеспеченность)», например Р=99% указывает, что расход воды обеспечен в 99 случаях из 100.

Иногда в расчетах используют термин повторяемость расходов воды в зависимости от водности года, обозначаемая m.

Соотношения величин обеспеченности Р (%)и повторяемости m представлены в Приложении 2.

Кривая обеспеченности обычно характеризуется тремя параметрами: средним

Qⁱ, коэффициентом вариации (изменчивости) СVи арифметическим значением ряда коэффициентом асимметрии СS. Эти параметры кривой распределения (обеспеченности) являются обычно вполне достаточными при решении гидрологических задач. С их помощью может быть установлена вероятность превышения или не превышения конкретного (заданного) значения стока (например, расхода воды).

Для вычисления величин, характеризующих кривую обеспеченности, используют методы математической статистики.

Среднее многолетнее значение расхода воды определяют по формуле n

Q )/ n. i

(3.2)

Коэффициент вариацииСV характеризует изменчивость ряда наблюдений и определяется по формуле

С

V

(3.3)

Коэффициент асимметрии СS характеризует несимметричность кривой

обеспеченности и определяется по формуле

С

S

(3.4)

Q

В этих формулах ⁱ – среднегодовое значение расхода воды; n – число лет гидрометрических наблюдений; k_i – модульный коэффициент года наблюдений i.

Гидрологические расчеты должны обеспечить достоверный прогноз появления тех или иных высоких расходов для проектирующегося моста или трубы в течение предстоящего многолетнего периода эксплуатации.

В качестве критерия при определении величины расчетной гидрологической характеристики для каждого вида строительства принимается ежегодная вероятность превышения (обеспеченность) этой величины, устанавливаемая нормативными документами.

Расчетные вероятности максимальных расходов для мостов и труб на железных и автомобильных дорогах приводятся в СНиП 2.05.03-84 «Мосты и трубы».

В соответствие со СНиП 2.05.03-84 вероятность превышения максимальных расходов паводков для мостовых переходов на железных дорогах I и II категорий общей сети принимается:

расчетных - Р=1,0 %; наибольших Р=0,33 %. Порядок решения задачи.

Обработка многолетнего ряда наблюдений начинается с ранжировки ряда, т. е. он выстраивается не хронологически, а в порядке уменьшения расходов.

Расчет интегральной кривой распределения ведется в табличной форме (табл. 2.3.2).

Таблица 2.3.2 - Расчет интегральной кривой распределения

Номера расходов в порядке их убывания	Максимальные годовые расходы в убывающем порядке Qi max , 3 м /с	Вероятность превышения Р i 100%	Модульные коэффициенты Q i kmax i Qmax	Отклонение модульных к оэффициентов от среднего ki 1	Квадратичное отклонение модульных коэффициентов от среднего (ki 2
1	2	3	4	5	6

Q^max - В этой таблице m – порядковый номер расхода, n – число наблюдений, среднее многолетнее значение максимальных расходов

)

n .

По расходам ранжированного ряда и соответствующим им вероятностям превышения Р(%) строится эмпирическая кривая распределения ежегодных вероятностей превышения.

Q f (Р%)

Эмпирическая кривая распределения ^max строится на клетчатках вероятностей (рис. 2.3.1), где по оси ординат откладывают расходы воды, а по оси абсцисс – соответствующие им значения вероятности превышения Р(%).

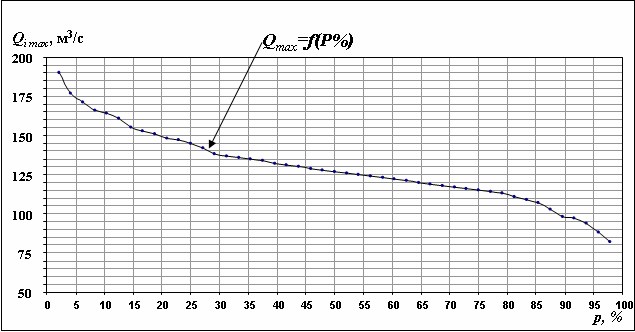
Рис. 2.3.1. Эмпирическая кривая распределения ежегодных вероятностей превышения

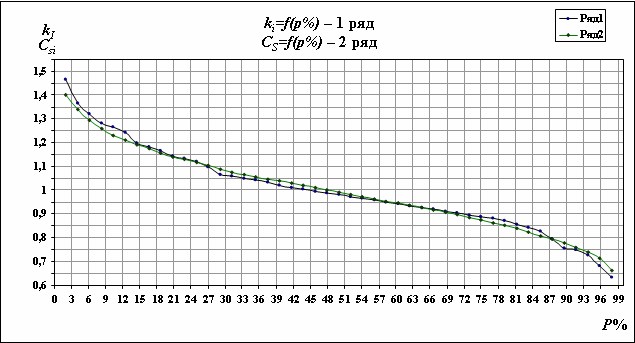
Рис. 2.3.2. Эмпирическая кривая распределения в модульных коэффициентах

Строится также эмпирическая кривая распределения в модульных коэффициентах, где вместо расходов на оси ординат откладывают модульные коэффициенты k_i (рис. 2.3.2).

Полученные точки соединяют плавной усредняющей кривой. Такая кривая распределения называется эмпирической.

Задачу предлагается решить двумя способами: аналитическим и графоаналитическим и сравнить полученные результаты.

Решение задачи аналитическим способом с использованием эмпирической кривой распределения.

На основании данных расчетов табл. 2.3.2 вычисляют характеристики кривой обеспеченности:

• среднее многолетнее значение максимального расхода определяют как среднеарифметическое значение максимальных расходов воды по формуле 3.2;

• коэффициент вариации (изменчивости расходов относительно их среднеарифметического значения) Сv определяют через безразмерные модульные коэффициенты по формуле 3.3;

• коэффициент асимметрии C_s, характеризующий несимметричность положения значений в ряду относительно их среднего значения, определяется по формуле 3.4.

Определяют расчетный расход заданной вероятности превышения (обеспеченности) по формуле

Q p% kP%Qmax _,

где k_p% - ордината кривой (рис. 2.3.2) для заданной вероятности превышения P=0,33%.

Решение задачи графоаналитическим методом с использованием биномиального распределения.

Используя эмпирическую кривую распределения ежегодных вероятностей превышения максимальных расходов воды (рис. 2.3.1) определяют расходы воды обеспеченностью 5, 50 и 95 %.

Вычисляют коэффициент скошенности по формуле

Q Q 2Q

S 5 95 50 .

Q Q

5 95 (20)

По коэффициенту скошенности, используя данные таблицы в приложении 2.3, находят коэффициент асимметрии максимальных расходов Сs и соответствующие ему нормированные отклонения ординат кривой обеспеченности от среднего значения при обеспеченностях 5, 50 и 95 %, т. е. Ф5, Ф50 и Ф95, а также разность Ф5 – Ф95 .

Вычисляют среднее квадратичное отклонение максимальных расходов воды по формуле

Q Q

5 95 .

Q Ф Ф

5 95 (3.5)

С редний многолетний максимальный расход воды находят по выражению Qmax Q50 Ф50 Q. (3.6)

^Q Q^max , определяют коэффициент вариации максимальных Зная величины и

расходов воды

C_V

^Qmax (3.7)

Q^max , C_v и Сs

По найденным параметрам теоретической кривой обеспеченности определяют расчетные максимальные расходы воды по выражению Q^p k^p Qmax, (3.8)

г де k_p – ордината теоретической кривой обеспеченности, определяемая по формуле k ФC 1

^{p v} (3.9)

Здесь Ф - нормированное отклонения ординат кривой обеспеченности от среднего значения при заданной обеспеченности, определяемое по таблице в приложении 2.3.

Для рассматриваемого случая k Ф С 1

0,33 0,33 v _;

Q0,33 k0,33 Qmax .

Полученное значение максимального расхода сравнивают с полученными результатами расчета по первому способу.