Приближенное решение задачи Коши обыкновенных дифференциальных уравнений первого порядка.

Постановка задачи. Найти приближенные значения решения обыкновенного дифференциального уравнения (ОДУ) на отрезке с шагом при начальном условии

1. Метод Эйлера:

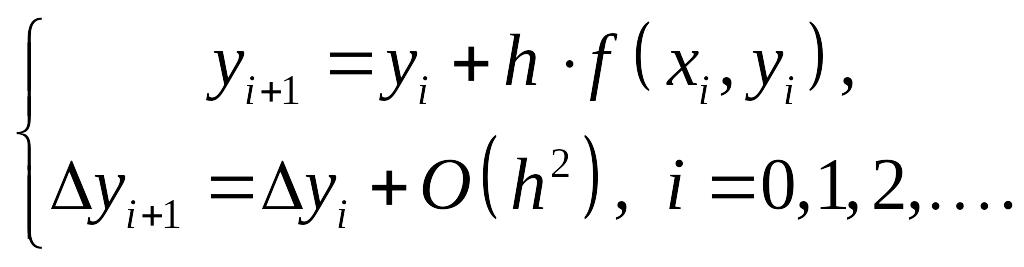
2. Усовершенствованный метод ломаных:

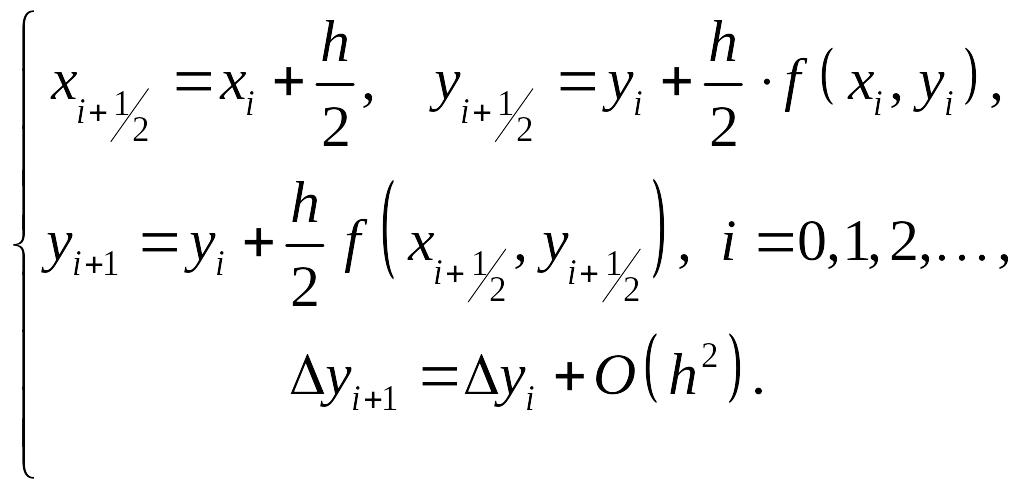
3. Метод Эйлера-Коши:

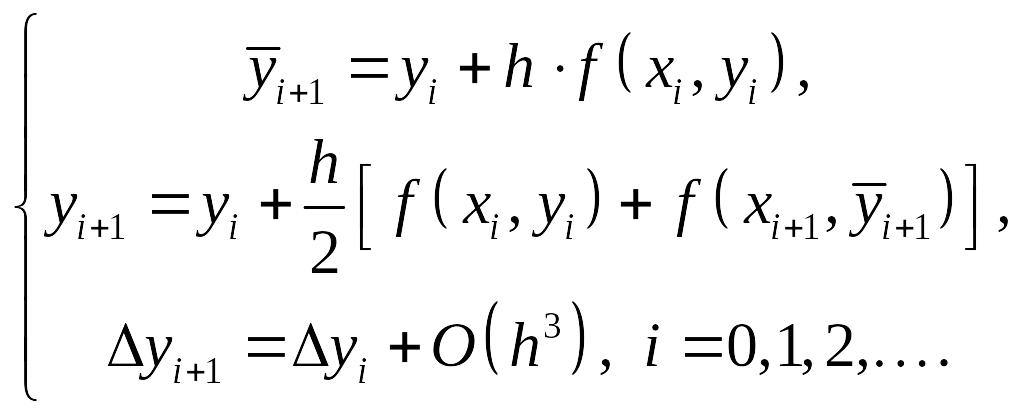
4. Метод Эйлера с уточнением:

.

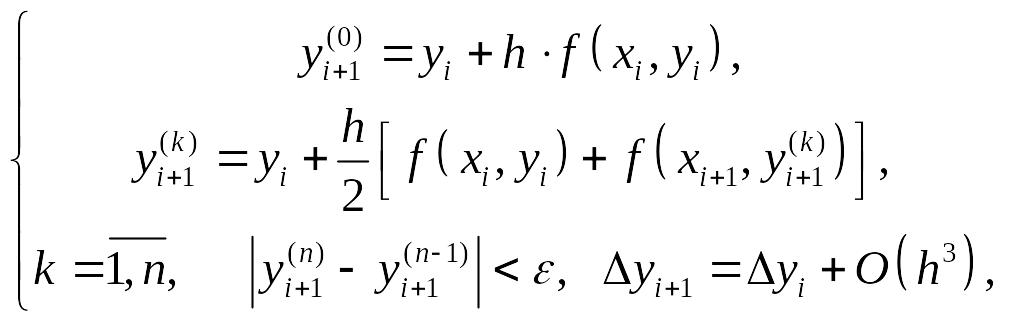
5. Метод Рунге-Кутта четвертого порядка

,

.

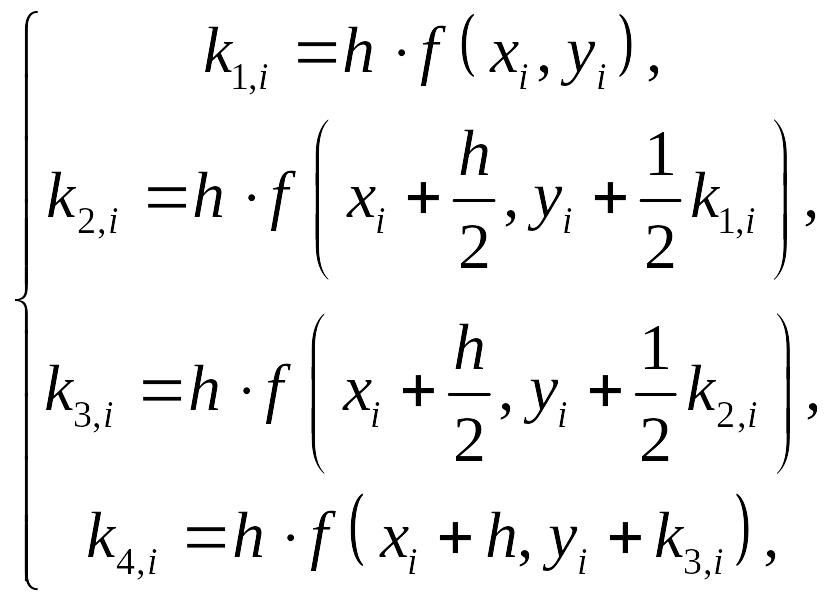
Лабораторная работа № 1

Тема: Решение нелинейных уравнений. Метод половинного деления.

Задание: 1) Отделить корни уравнения графически и программно .

2) Уточнить корни (все!) уравнения методом половинного деления с точностью , указать число разбиений отрезка.

Вопросы самоконтроля.

1. Как отделяются корни уравнения?

2. Какой должна быть величина шага при отделении корней?

3. Какие условия должны быть выполнены для применения метода половинного деления отрезка?

4. Какова идея метода половинного деления отрезка? Геометрическая иллюстрация.

5. Как вычисляется приближенный корень уравнения и какова его погрешность?

6. Как зависит погрешность результата от выбора приближенного решения?

Вариант	Уравнение		Вариант	Уравнение
1			31
2			32
3			33
4			34
5			35
6			36
7			37
8			38
9			39
10			40
11			41
12			42
13			43
14			44
15			45
16			46
17			47
18			48
19			49
20			50
21			51
22			52
23			53
24			54
25			55
26			56
27			57
28			58
29			59
30			60