
- •Краткая теория к лабораторным и контрольным работам Приближенное решение нелинейного уравнения
- •Метод половинного деления.
- •Метод хорд.
- •Метод Ньютона (метод касательных).
- •Метод итерации.
- •Метод хорд и касательных.
- •Приближенное решение системы линейных алгебраических уравнений
- •Интерполирование функций полиномом.
- •Приближенное решение обратной задачи интерполирования
- •Приближенное дифференцирование
- •Численное интегрирование
- •Приближенное решение задачи Коши обыкновенных дифференциальных уравнений первого порядка.
- •Метод Рунге-Кутта четвертого порядка
- •Лабораторная работа № 1
- •Образец выполнения лабораторной работы № 1
- •Лабораторная работа № 2
- •Образец выполнения лабораторной работы № 2
- •Лабораторная работа № 3
- •Лабораторная работа № 4
- •Лабораторная работа № 5
- •Образцы выполнения заданий лабораторных работ №3-5
- •Лабораторная работа № 6
- •Образец выполнения лабораторной работы № 6
- •Лабораторная работа № 7
- •Образец выполнения лабораторной работы № 7
- •Лабораторная работа № 8
- •Образец выполнения лабораторной работы №8
- •Лабораторная работа № 9
- •Образец выполнения лабораторной работы №9
- •Лабораторная работа № 10
- •Образец выполнения лабораторной работы №10
- •Лабораторная работа № 11
- •Образец выполнения лабораторной работы №11
- •Лабораторная работа № 12
- •Образец выполнения лабораторной работы №12
- •Темы домашних контрольных работ
- •Задание к домашней контрольной работе №1
- •Элементы теории погрешностей.
- •Раздел 3. Темы для вычислительного практикума
- •Методы решения нелинейных уравнений.
- •Методы решения систем линейных уравнений.
- •Методы решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка (оду).
- •Методы решения краевых задач для оду.
- •Метод сеток для дифференциальных уравнений в частных производных.
- •Список литературы
Форма отчёта:
Постановка задач. Краткая теория (метод решения). Геометрическая интерпретация.
Алгоритм решения поставленной задачи. (Блок-схема).
Текст программы.
Тестовый пример.
Численный расчёт по данным исходной задачи с оценкой погрешности результата. Протокол работы программы.
Анализ полученного результата.
Пояснения к отдельным пунктам отчета.
Постановка задачи включает краткую математическую формулировку задачи с пояснением отдельных моментов, а также необходимые графики и/или рисунки. Должны быть приведены основные моменты применяемых методов.
Алгоритм решения задачи может быть оформлен или в виде блок-схемы, или в словесной форме. Допускается описание алгоритма осмысленными частями (блоками).
Текст программы численного решения задачи должен быть написан на предлагаемом языке программирования, который может быть изменен по согласованию с преподавателем данного курса.
Под тестовым примером или тестом понимается задача (аналогичная по постановке искомой задаче) у которой известно точное решение, что позволяет сравнить численные результаты (приближенное и точное решения) и оценить допускаемую погрешность. По результатам тестирования должен быть сделан вывод.
Протокол работы программы должен включать результаты как по тестовому примеру, так и численного расчета искомой задачи. Результаты численных расчетов должны быть оформлены по всем правилам записи приближенных чисел, т.е. запись приближенного решения только с верными значащими цифрами и допускаемой погрешностью.
Анализ численных результатов должен дать ответ на вопрос, соответствуют ли полученные результаты искомому решению поставленной задачи и почему.
Краткая теория к лабораторным и контрольным работам Приближенное решение нелинейного уравнения
Метод половинного деления.
Постановка задачи. Дано нелинейное
уравнение
![]() ,
где функция
,
где функция
![]() определена и непрерывна для всех
определена и непрерывна для всех
![]() ,
причем функция меняет знак на концах
этого отрезка, т.е.
,
причем функция меняет знак на концах
этого отрезка, т.е.
![]() .
.
Найти приближенное решение данного
уравнения
с точностью
![]() ,
а так же необходимое для этого число
разбиений отрезка
,
а так же необходимое для этого число
разбиений отрезка
![]() .
.
Приближенное решение
![]() и погрешность приближения
и погрешность приближения
![]() находятся по следующей схеме:
находятся по следующей схеме:
![]() ,
,
![]() ,
,
![]() ;
;
где
![]() ,
удовлетворяет условиям
,
удовлетворяет условиям
![]() ,
,
![]() ;
из последнего определяется число
разбиений отрезка
;
из последнего определяется число
разбиений отрезка
![]() .
.
Метод хорд.
Постановка задачи. Дано нелинейное уравнение , где функция определена и непрерывно-дифференцируема для всех , причем функция меняет знак на концах этого отрезка, т.е. .
Найти приближенное решение данного уравнения с точностью .
Приближенное решение и погрешность приближения находятся по следующей схеме:
если
![]() на
,
то
на
,
то
![]() ,
,
![]() ,
,
![]() ;
;
если
![]() на
,
то
на
,
то
![]() ,
,
![]() ,
.
,
.
Приближенное решение и погрешность приближения :
![]() ,
,
![]() .
.
Метод Ньютона (метод касательных).
Постановка задачи. Дано нелинейное уравнение , где функция определена и непрерывно-дифференцируема для всех , причем функция меняет знак на концах этого отрезка, т.е. .
Найти приближенное решение данного уравнения с точностью .
Приближенное решение и погрешность приближения находятся по следующей схеме:
![]() ,
;
,
;
если на , то ;
если на , то .
Приближенное решение и погрешность приближения :
, .
Метод итерации.
Постановка задачи. Дано нелинейное уравнение, где функция определена и непрерывно-дифференцируема для всех , причем функция меняет знак на концах этого отрезка, т.е. .
Найти приближенное решение данного уравнения с точностью .
Приближенное решение и погрешность приближения находятся по следующей схеме:
уравнение приводится к виду
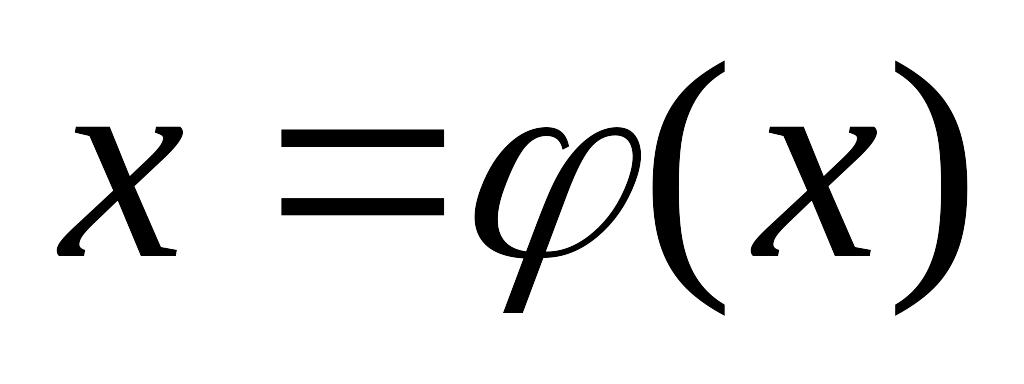 ,
где функция
,
где функция
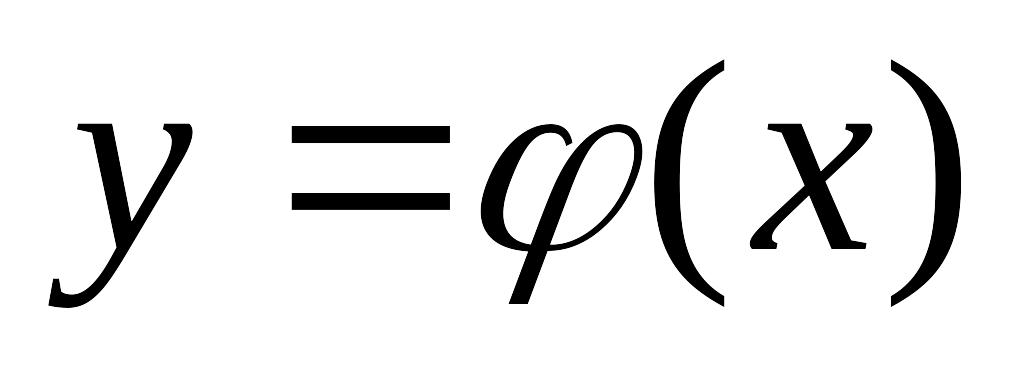 удовлетворяет условиям:
удовлетворяет условиям:
 ,
дифференцируема на данном отрезке и
,
дифференцируема на данном отрезке и
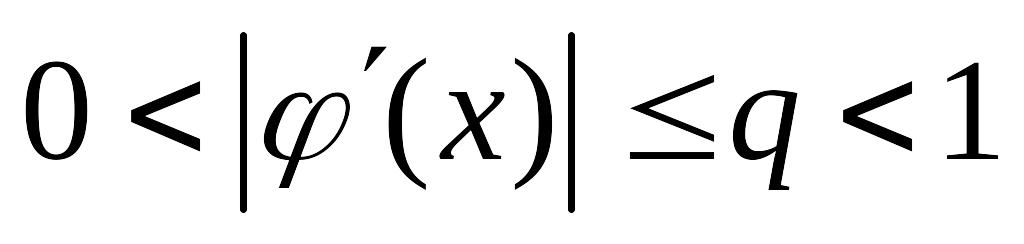 ;
;строится итерационная последовательность вида
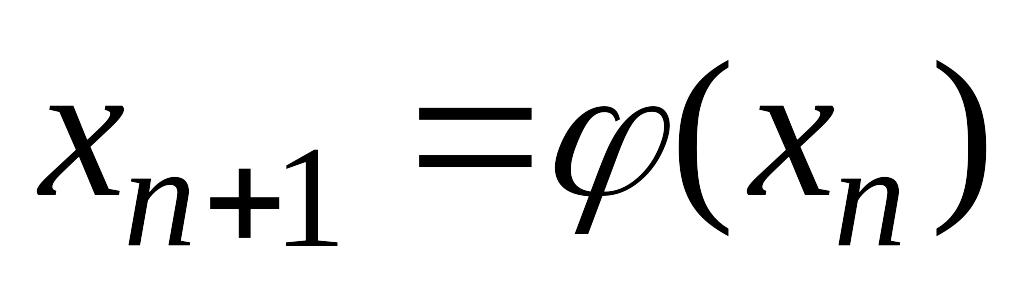 ,
,
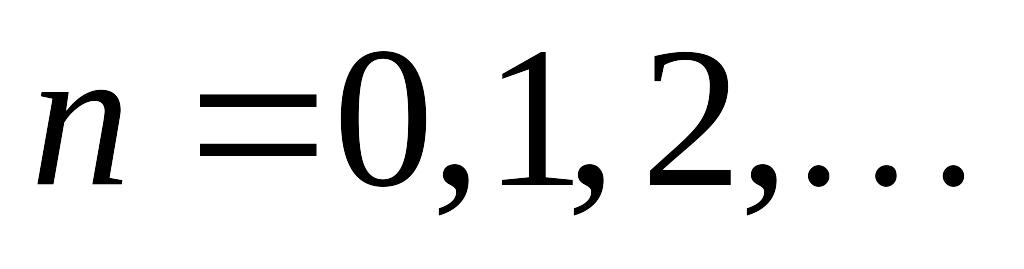 ,
где
,
где
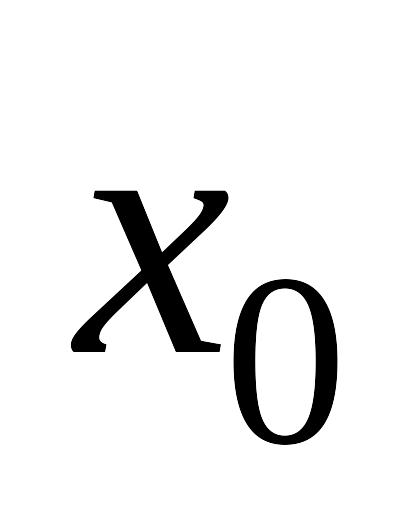 выбирается произвольно из данного
отрезка, например,
выбирается произвольно из данного
отрезка, например,
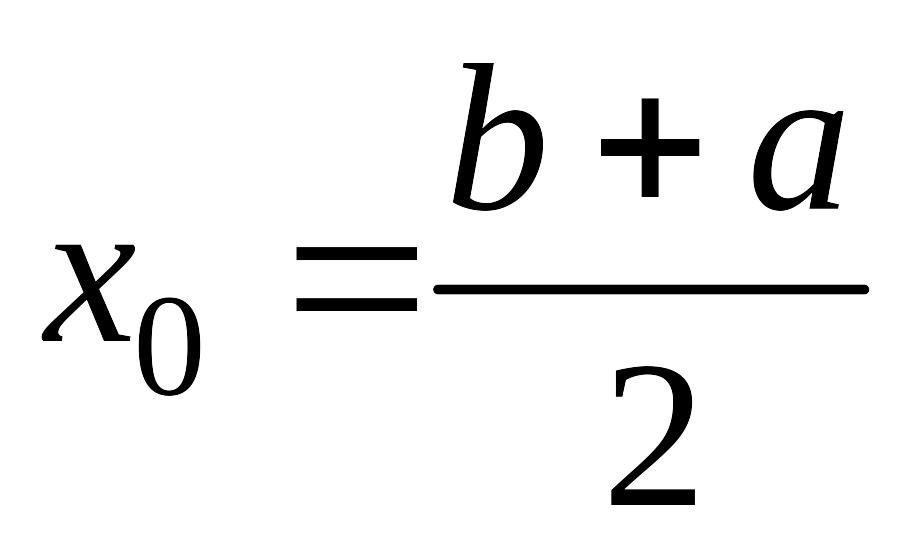 ;
;полагая
 приближенное значение корня
приближенное значение корня
 ,
для погрешности получим
,
для погрешности получим
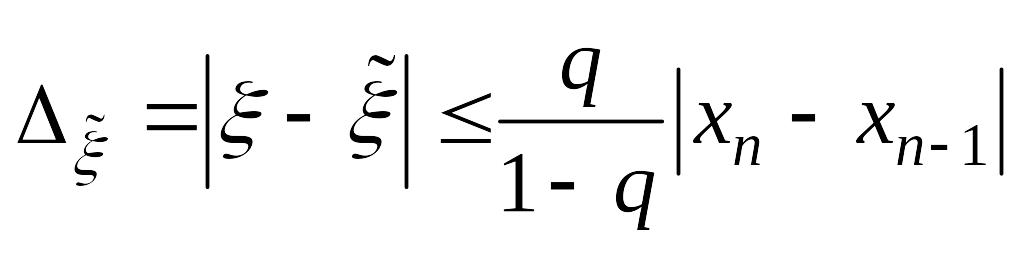 ,
а так как по условию
,
а так как по условию
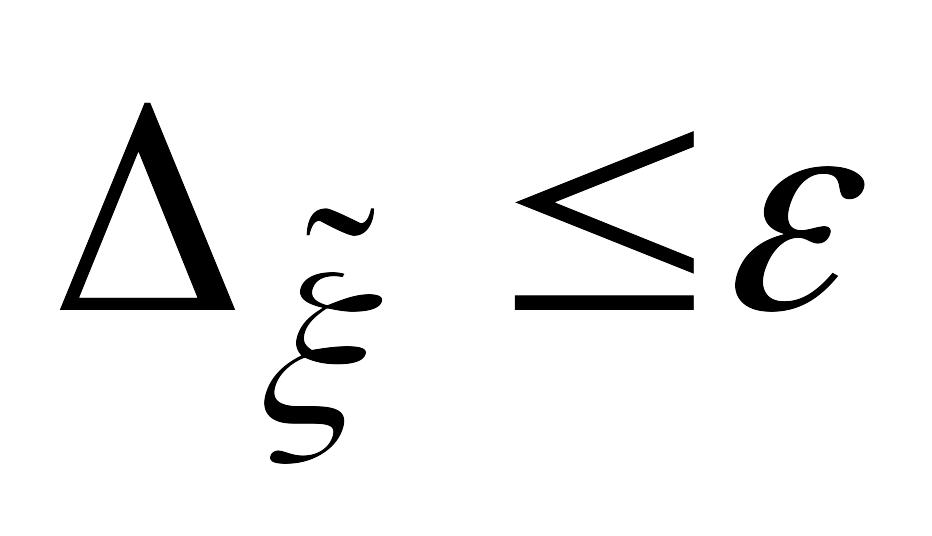 ,
то итерационный процесс продолжим до
выполнения условия
,
то итерационный процесс продолжим до
выполнения условия
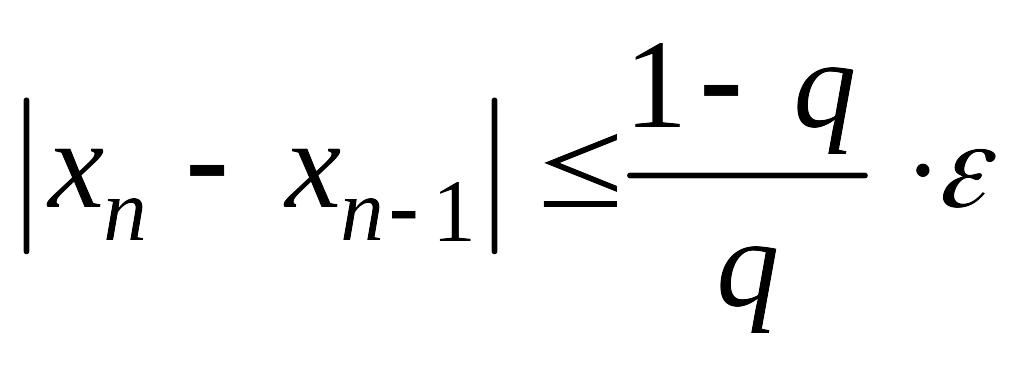 ,
при этом приближенное значение корня
определяется как
.
,
при этом приближенное значение корня
определяется как
.
Приближенное решение и погрешность приближения :
,
![]() .
.
Метод хорд и касательных.
Постановка задачи. Дано нелинейное уравнение, где функция определена и непрерывно-дифференцируема для всех , причем функция меняет знак на концах этого отрезка, т.е. .
Найти приближенное решение данного уравнения с точностью .
Приближенное решение и погрешность приближения находятся по следующей схеме:
если на , то
,
![]() ,
,
![]() ,
,
![]() ,
;
,
;
если на , то
,
![]() ,
,
![]() ,
,
![]() ,
.
,
.
Приближенное решение и погрешность приближения :
![]() ,
,
![]() .
.
Приближенное решение системы линейных алгебраических уравнений
Постановка
задачи. Найти приближенное
решение системы линейных алгебраических
уравнений
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Если
![]() ,
то система имеет единственное решение.
,
то система имеет единственное решение.
Явный метод итерации. Представим данную систему в виде приведенной системы
![]() ,
,
где
![]() ,
,
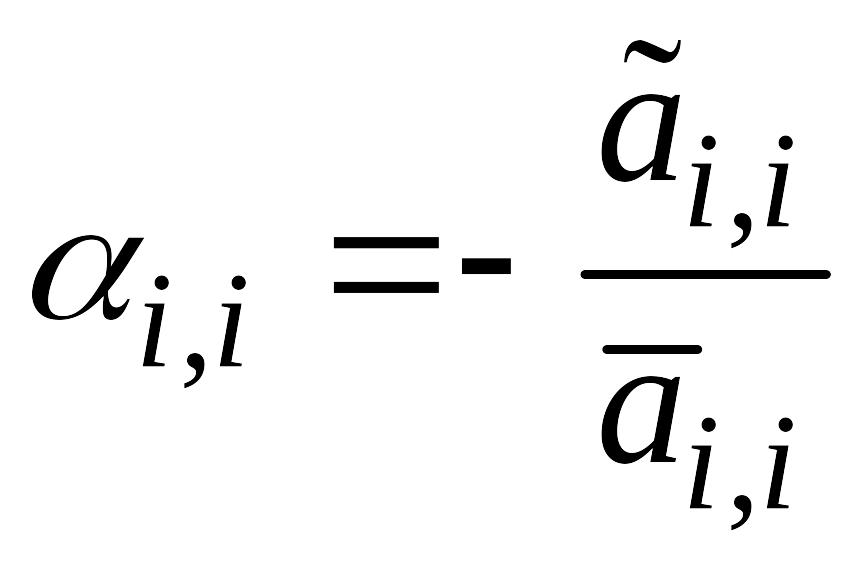 ,
,
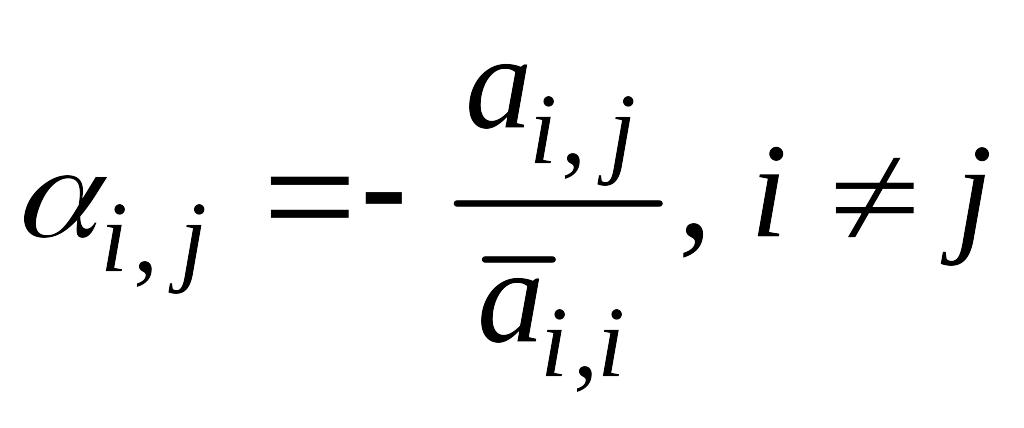 ,
,
![]() ,
,
![]() ,
;
,
;![]() .
.
Приближенное решение ищем по следующей итерационной схеме
![]()
![]() ,
,
![]() или
или
![]() ,
,
,
,
![]() .
.
Для
сходимости итерационной последовательности
необходимо выполнение следующего
условия:
![]() .
Где
.
Где
![]() канонические нормы:
канонические нормы:
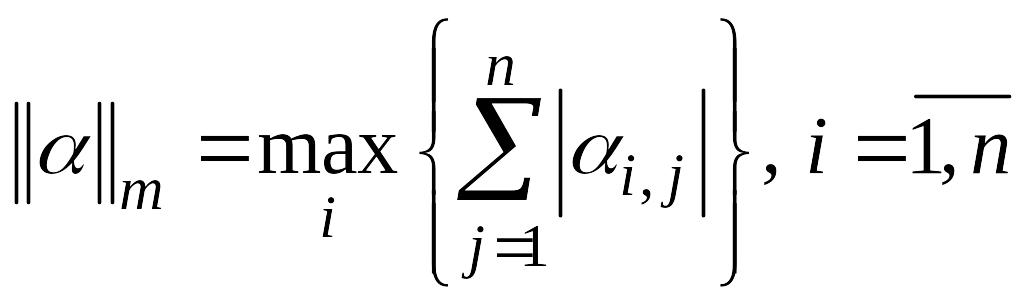 ;
;
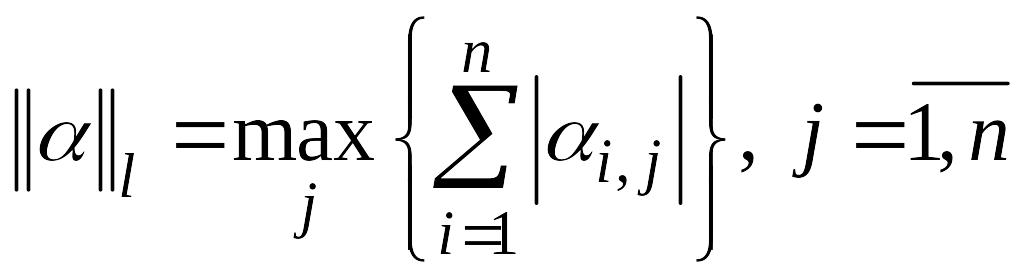 ;
;
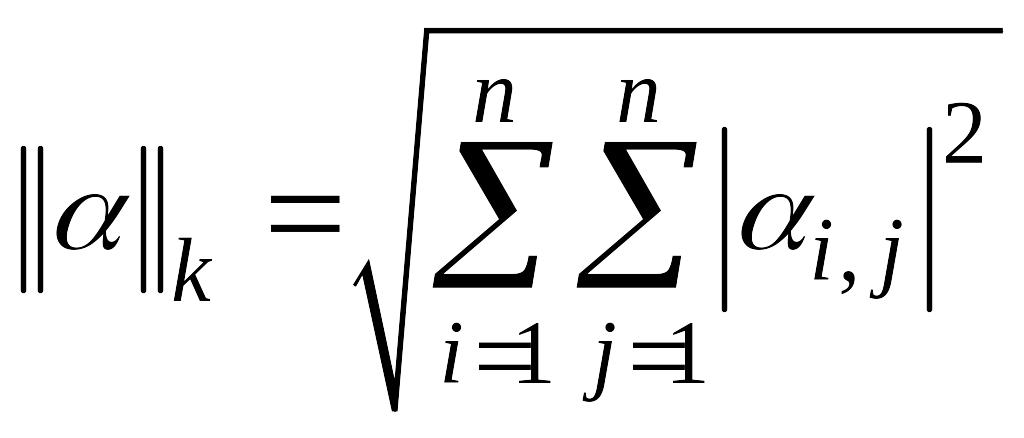 .
.
Итерационная последовательность продолжается до выполнения условия
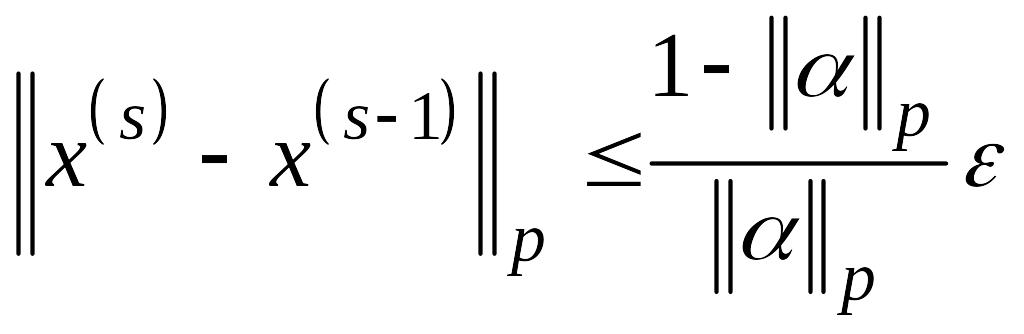 ,
,
,
,
![]() .
.
Тогда за приближенное решение можно взять
![]() ,
,
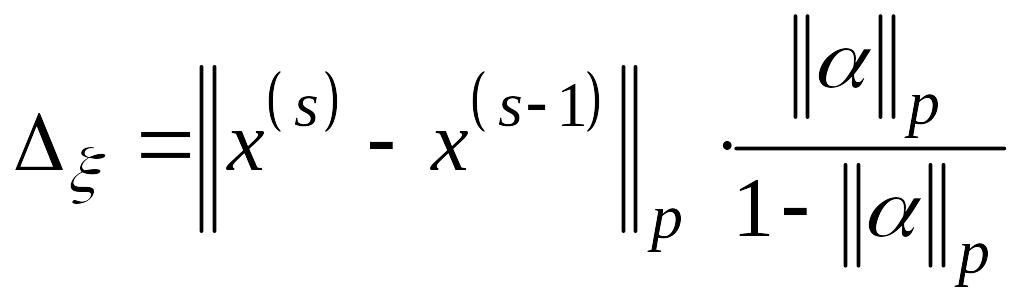 .
.
Явный метод Зейделя. По данному методу приближенное решение ищется по следующей схеме
![]() ,
,
![]() .
.
Определение сходимости и оценка погрешности производится так же, как и для метода итерации.
