2.2 Завдання №2
- Згідно номеру варіанту таблиці 6 (номер у журналі) обрати завдання для коду РС 31,16
- Аналітично – графічним методом реалізувати ці завдання:
- Згідно номеру варіанту таблиці обрати номер інформаційного пакету (рисунок 1), внести помилку у відповідний біт і виправити цю помилку аналітично – графічним методом. Запустити файл Corr3116.exe та порівняти теоретичні розрахунки з практичними
Таблиця 6
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
29 |
30 |
31 |
|
||||
Пакет Біт |
№1 №1 |
№2 №15 |
№3 №14 |
№4 №13 |
№5 №12 |
№6 №11 |
№7 №10 |
Пакет Біт |
№8 №9 |
№9 №8 |
№10 №7 |
№11 №6 |
№12 № 5 |
№13 №4
|
№14 №t3 |
Пакет Біт |
№15 №2 |
№16 №1 |
№15 №30 |
№14 №30 |
№13 №29 |
№12 №28 |
№11 №27
|
Пакет Біт
|
№10 №26 |
№9 №25 |
№8 №24 |
№7 №23 |
№6 №22 |
№5 №21 |
№4 №20
|
Пакет Біт
|
№3 №19 |
№1 №15 |
№2 №18 |
|
|
|
|
Приклад виконання варіанту №30
Теоретично виправимо помилку кратності 1, яка виникла у послідовному каналі зв’язку при передачі інформації кодом РС31,16. Поліном, що не приводиться, для побудови матриці G 31,16 має вигляд Р(х15)=х15+х11+х10+х9+х8+х7+х5+х3+х2+х+1
Тож матриця, що народжує для коду РС31,16 набуде наступного вигляду:
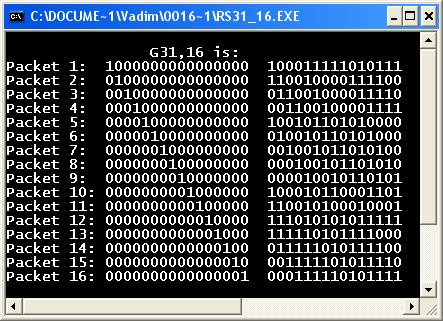
Перевірочна матриця H набуде наступного вигляду:
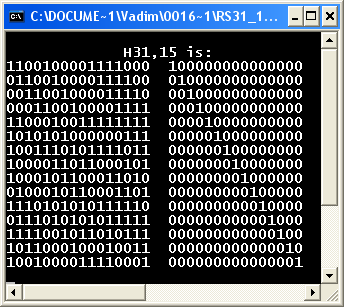
На підставі перевірочної матриці Н31,15 система лінійних незалежних рівнянь буде такою:
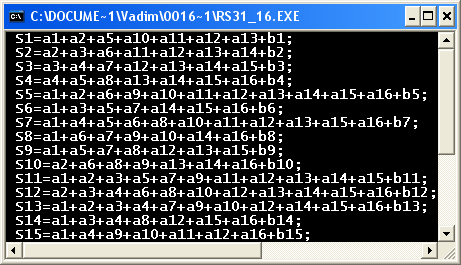
Згідно з варіантом №30 візьмемо дозволений пакет №1 (f(x)) з матриці, що народжує (рисунок 1) і внесемо помилку кратності 1 у інформацій біт (біт №15 за порядковим номером зправа наліво, починаючи з нульового - помічено червоним кольором ):
f’(x)=0000000000000001 100011111010111
Упевнимося, що комбінація є хибною (поділимо прийняту комбінацію f’(x) на поліном, що не приводиться Р(х15)=х15+х11+х10+х9+х8+х7+х5+х3+х2+х+1, або Р(1,0)=1000111110101111:
Залишок від ділення R(7)<>0. Це свідчить, що при передачі пакету даних у каналі зв’язку трапилася помилка.
Для того щоб зрозуміти якої кратності трапилися помилка потрібно спочатку обчислити синдром для помилки кратності 1.
У відповідності з системою лінійних незалежних рівнянь на підставі прийнятої хибної комбінації f’(x) обчислимо синдром, при чому знак «+» означає виконання операції додавання за модулем 2:
S1=1+0+0+0+0+0+0+1=0;
S2=0+0+0+0+0+0+0+0=0;
S3=0+0+0+0+0+0+0+0=0;
S4=0+0+0+0+0+0+1+0=1;
S5=1+0+0+0+0+0+0+0+0+0+1+1=1;
S6=1+0+0+0+0+0+1+1=1;
S7=1+0+0+0+0+0+0+0+0+0+1+1=1;
S8=1+0+0+0+0+0+1+1=1;
S9=1+0+0+0+0+0+0+1=0;
S10=0+0+0+0+0+0+1+0=1;
S11=1+0+0+0+0+0+0+0+0+0+0+1=0;
S12=0+0+0+0+0+0+0+0+0+0+1+0=1;
S13=1+0+0+0+0+0+0+0+0+0+1+1=1;
S14=1+0+0+0+0+0+1+1=1;
S15=1+0+0+0+0+0+1+1=1;
Тож обчислений синдром у нашому випадку має наступний вигляд:
S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 S11 S12 S13 S14 S15= 000111110101111
З
вернемося
до заздалегідь обчислених синдромів
помилок кратності 1 для відповідних
бітів (№ біта + 1):
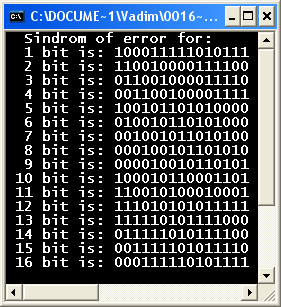
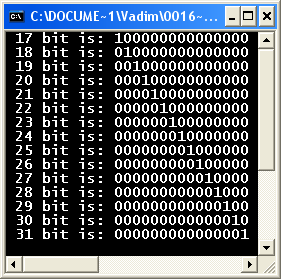
Знайдемо обчислений синдром на рисунку і визначимо помилку кратності 1 у біті за номером 15. Тож вектор помилки е(х) набуде наступного вигляду:
е(1,0)=000000000000000100000000000000
Розкриємо практичну сторону тематичного контролю знань 2. Запустимо тестову програму CORR3116.exe і введемо хибну комбінацію f’(x):
Слід відмітити, що у векторі помилки одиниця розташована на 15 позиції і показує на помилку .
Якщо ввести безпомилкову комбінацію:
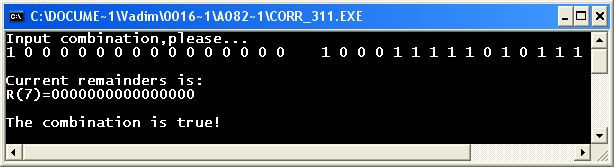
Отримаємо підтвердження, що введена комбінація є істиною.
У випадку виникнення помилки більше кратності 1, отримаємо повідомлення про фатальну помилку:
