17) Распределенность терминов в суждении
технич. выражение, используемое традиц. логикой в теории суждения и умозаключения. Говорят, что термин распределен, если он мыслится во всем объеме. Во всех остальных случаях термин наз. нераспределенным. Напр., в суждении "все квадраты – прямоугольники" термин "квадрат" – распределен, поскольку в данном суждении речь идет о всем объеме понятия "квадрат", т.е. о всех квадратах. Приняты след. правила Р. т. в с.: субъект суждения распределен во всех общих суждениях и не распределен в частных суждениях, предикат суждения распределен во всех отрицат. суждениях и не распределен в утвердит. суждениях. Обычно эти правила иллюстрируются с помощью кругов Эйлера, представляющих объемы понятий (классы). Напр., Р. т. в с. вида "все S суть P", в к-ром класс S целиком включается в класс P, изображается след. образом:
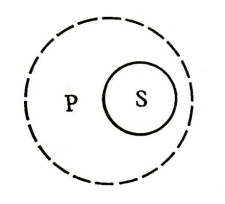
Для наглядности класс S ограничен сплошной линией, т.к. имеются в виду все S, а класс Ρ – пунктирной линией, т.к. неизвестно, каковы границы класса P: в зависимости от конкретного значения Ρ он может или совпадать с S ("все квадраты – прямоугольники с равными сторонами"), или быть больше S по объему ("все квадраты – параллелограммы"), но S всегда совпадает по крайней мере с частью Р.
Устанавливая правила Р. т. в с., иногда принимают во внимание деление суждений на выделяющие и невыделяющие. В связи с этим правила Р. т. в с. общеутвердительных и четноутвердительных формулируются несколько иначе. Однако следует учитывать, что проблема Р. т. в с. этого типа носит особый характер, поскольку предполагает привлечение дополнит. сведений об отношении классов S и P, и что, следовательно, ее нельзя смешивать с проблемой Р. т. в с., взятом безотносительно к упомянутым дополнит. сведениям.
18) Логические операции с суждениями
Логические операции с суждениями затрагивают их типы и виды, их субъектно-предикатную структуру и т. д. Среди данных операций выделяют две наиболее общие и важные группы: преобразование простых и сложных суждений и отрицание данных суждений.
Преобразование суждений – выяснение точного логического смысла суждения. Это достигается посредством таких логических операций, как обращение, превращение, противопоставление субъекту и противопоставление предикату.
Обращение (конверсия) – это преобразование суждения путем перестановки его субъекта и предиката местами, в результате чего предикат суждения становится субъектом, а субъект – предикатом. При этом количество суждения может изменяться, а качество не меняется. Например: «Все адвокаты – юристы». В результате замены субъекта и предиката друг другом получится следующее суждение: «Некоторые юристы – адвокаты».
В основе обращения лежит сходство содержания тех понятий, которые обмениваются местами в обращаемом суждении. Именно данное сходство делает возможным перестановку понятий субъекта и предиката в обращенном суждении. Любое определение, выраженное общим суждением, может быть обращено. При этом суждение остается общим.
Превращение (обверсия) – это преобразование суждения путем перемены его качества на противоположное. Количество суждения, его субъект и предикат при этом не меняются. Например: «Все адвокаты – юристы». Посредством превращения данное суждение преобразовывается в следующее: «Ни один адвокат не является неюристом».
Превращение – это преобразование формы суж-Хдения.
Противопоставление субъекту – преобразование суждения путем обращения и последующего превращения. Например, если суждение «Все адвокаты – юристы» сначала обратить в суждение «Некоторые юристы – адвокаты», а последнее в свою очередь обратить в суждение «Некоторые юристы не есть неадвокаты», то получится противопоставление субъекту. Предикат заключительного суждения – «неадвокаты» – противопоставляется субъекту исходного суждения – «адвокаты».
Противопоставление предикату – преобразование суждения путем обращения и последующего превращения. Например, суждение «Все адвокаты – юристы» превратить в суждение «Ни один адвокат не является неюристом», а последнее обратить в суждение «Ни один неюрист не является адвокатом». Получается, что предикату исходного суждения «юристы» противопоставлено понятие «неюристы».
Другую важнейшую операцию представляет собой отрицание суждений, или инверсия. Его сходство с преобразованием состоит в том, что результатом отрицания тоже выступает новое суждение. Отличие же состоит в том, что в процессе отрицания суждения не только его форма, но и смысл. Таким образом, в основе отрицания суждений лежит их несовместимость. Например: «Все судьи справедливы» – «Неверно, что все судьи справедливы».
Отрицания нельзя сравнивать с отрицательными суждениями. Когда говорится об отрицательном суждении, то имеется в виду один вид суждения по характеру связки. Когда говорится об отрицании, то подразумевается особая логическая операция с суждениями.