Числа Бернулли

Числа Бернулли — последовательность рациональных чисел B₀,B₁,B₂,... найденная Я. Бернулли в связи с вычислением суммы одинаковых степеней натуральных чисел:

B0 = 1

B3 = 0

B5 = 0

B7 = 0

B9 = 0

B11 = 0

B13 = 0

B15 = 0

Формула для чисел Бернулли

Для чисел Бернулли существует следующая реккурентная формула:

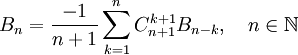
Свойства

• Все числа Бернулли с нечетными номерами, кроме B₁, равны нулю, знаки B_2n чередуются.

• Числа Бернулли являются значениями при x = 0 многочленов Бернулли: B_n = B_n(0).

Коэффициентами разложения некоторых элементарных функций в степенные ряды часто служат числа Бернулли. Например:

• Экспоненциальная производящая функция для чисел Бернулли:

,

• ,

• .

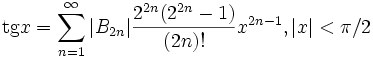• Эйлер указал на связь между числами Бернулли и значениями дзета-функции Римана ζ(s) при четных s = 2m:

Из чего следует

B_n = − nζ(1 − n) для всех n.

Заключение

Изучение чисел с собственными именами закончено, но ненадолго. Изучая эту тему я нашла еще больше таких чисел, например: Числа Мерсенна, Числа Ферма и т.п. Эти числа менее известны, но в будущем я собираюсь изучить и их. Эта тема увлекательна и непостижима одновременно, так как невозможно изучить все числа. Благодаря чему становиться намного приятней осознавая, что хоть чуть-чуть приближаешься к чему то совершенному и непостижимому.

Я считаю, что задача поставленная мной вначале работы выполнена.

Приложение. Числа с именем.

Числа Мерсенна - М_р = 2^р – 1, р-простое число. При некоторых значениях р М_р также простое число.

Числа Ферма - F_k =2² + 1, k N. При некоторых значениях k F_k – простые числа. F_1, F₂, F₃ - простые числа; F₄ = 2³² + 1 – составное, один из делителей – 641.

Числа Евклида - E_k = 2^k-1(2^k-1), k N.

Палиндромическое число - число, записанное теми же цифрами, но в обратном порядке. Например: 3805, палиндром – 5083.

Совершенное число - число равное сумме всех своих собственных делителей (т. е. делителей отличных от самого числа). Например, число 28 – совершенное: его делители 1, 2, 4, 7, 14 . Число 28 = 1+2+4+7+14. Если при натуральном k число 2^k – 1 простое, то число Евклида 2^k-1(2^k – 1) совершенное. Исследователи нашли уже более 30 совершенных чисел, 6, 28, 496, 8128, 33 550 336 и др. Почти все последующие совершенные числа выдерживают только евклидову форму записи, вот 25-е: 2^{44 496}(2^{44 497} – 1).

Дружественные числа - пара чисел, обладающих таким свойством: сумма собственных делителей первого из них равна второму числу, а сумма собственных делителей второго числа равна первому числу. Например, сумма делителей числа 220 равна 1+2+4+5+10+11+20+22+44+55+110=284, а сумма делителей числа 284 равна 1+2+4+71+142=220, поэтому числа 220 и 284 – дружественная пара. Вторая дружественная пара – 1184 и 1210 была найдена в 1867 году шестнадцатилетним итальянцем Б.Паганини.

Шахматное число - Число 2⁶⁴-1

Магическая константа - постоянная сумма чисел в каждой строке магического квадрата n x n. Определяется формулой 0,5n(n² + 1)

Числа Армстронга - натуральное число из n цифр является числом Армстронга, если сумма его цифр, возведённая в n-ую степень равна самому числу.

Например, 153= 1³+5³+3³.

Пифагоровы тройки чисел - все такие тройки натуральных чисел a, b, c, что a²+b²=c².