4.3. Обобщенная модель нелинейной однофакторной регрессии

В этом параграфе рассмотрим общий случай регрессионной модели, нелинейной относительно фактора x, но линейной относительно неизвестных коэффициентов.

Предположим, что зависимость переменной y от фактора x имеет вид:

. (4.3.1)

В уравнении (4.3.1) , известные нелинейные функции переменной x; , - неизвестные коэффициенты. Случайные составляющие по-прежнему предполагаются нормально распределенными случайными величинами с нулевыми средними, одинаковыми (неизвестными) дисперсиями s² и независимыми друг от друга.

Функция регрессии будет иметь вид:

. (4.3.2)

Для нахождения неизвестных коэффициентов модели (4.3.1) опять воспользуемся линеаризацией этой функции и приведением ее к модели многофакторной линейной регрессии. Произведем замену переменных следующим образом:

,

,

………..

.

Тогда вместо уравнения (4.3.1) мы можем записать следующее уравнение линейной многофакторной регрессионной модели:

. (4.3.3)

Один из методов оценивания параметров линейной многофакторной регрессии – МНК, мы уже рассмотрели в третьей главе. Воспользуемся полученными там результатами и сразу запишем систему нормальных уравнений в матричной форме. Для этого введем в рассмотрение следующие матрицы и векторы:

= ;

, .

Матричное уравнение вида (3.1.8) с учетом введенных обозначений запишется в виде:

. (4.3.4)

Если квадратная матрица размерности будет невырожденной, то решение матричного уравнения (4.3.4) существует и его можно найти по формуле:

. (4.3.5)

Так как по формуле (4.3.5) находим не сам вектор неизвестных b, а его оценку, полученную по МНК, то равенство (4.3.5) будет корректно переписать в виде:

, (4.3.6)

где В - это вектор оценок: .

Качество аппроксимации результатов наблюдений функцией регрессии:

(4.3.7)

определяют при помощи величины , которая является оценкой дисперсии s². Оценка вычисляется по формуле:

= .(4.3.8)

С учетом введенных ранее обозначений для вычисления можно воспользоваться формулой:

= . (4.3.9)

Если модель (4.3.1) адекватна эмпирическим данным, то является несмещенной оценкой дисперсии ².

Отметим также, что случайная величина распределена по закону с (n-k) степенями свободы. Этот факт используется при построении доверительного интервала для s² , он имеет вид:

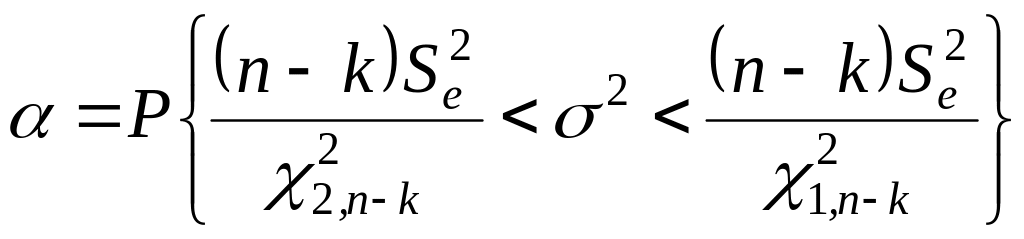. (4.3.10)

Значения и ищут по таблицам критических точек распределения по заданной доверительной вероятности и (n -k) степеням свободы.

В свою очередь, границы доверительных интервалов для неизвестных коэффициентов находят по следующим формулам

.(4.3.11)

В формуле (4.3.11) использованы следующие обозначения: - диагональный элемент матрицы с номером (j+1,j+1), -значение симметричной квантили порядка a, найденное по таблицам распределения Стьюдента по заданной доверительной вероятности a и (n- k) степеням свободы, .

Алгоритм проверки гипотезы о значимости модели с использованием статистики Фишера будет следующим. Выдвигаем основную и альтернативную гипотезы вида:

Для проверки основной гипотезы Н₀ вводим выборочную статистику Z*:

, (4.3.12)

которую можно записать и в следующем виде:

. (4.3.13)

Если основная гипотеза верна, то случайная величина Z* распределена по закону Фишера с n₁=(k-1), n₂=(n-k) степенями свободы: Z*=F_k-1,n-k.. Границу правосторонней критической области K₂ находят по таблицам распределения Фишера по заданному уровню значимости 1-a и n₁=(k-1), n₂=(n-k) степеням свободы. В том случае, если Z*³ K₂, гипотезу H₀ отвергаем и делаем вывод, что выбранная регрессионная модель статистически значима. Принимаем основную гипотезу H₀ и считаем, что модель (4.3.1) статистически незначима, если

0<Z*< K₂.

Пример 4.3.1. Для того чтобы инвестиционный менеджер мог правильно выбрать время операции (market timer), для прогнозирования изменения избыточной доходности портфеля ценных бумаг в зависимости от избыточной доходности, рынка ему приходится использовать не только линейную регрессионную модель, но и более сложные модели [16]. Рассмотрим в качестве примера такой зависимости квадратичную функцию:

.

В последнем уравнении использовались следующие обозначения:

● - избыточная доходность рынка в момент времени i;

●( ) -избыточная доходность портфеля ценных бумаг в момент времени i;

● - безрисковая ставка доходности;

● - случайная составляющая.

Пусть , = , у = ( ). Тогда исходное уравнение перепишем в виде:

.

Запишем вид матрицы Н для этой модели:

Н= .

В качестве упражнения, используя исходные данные примера 2.5.1, оцените параметры нелинейной регрессии и проведите ее статистическое тестирование двумя способами. Во-первых, применяя формулы (4.3.6)-(4.3.13), во-вторых, используя результаты функции «РЕГРЕССИЯ» для линеаризованной модели. Сопоставьте полученные результаты. ▲