Частные случаи.

1. Для вакуума μ_а=μ₀, ε_а=ε₀, σ=0 и δ=0. В соответствии с (5), (7), (8) коэффициент затухания, фазовая скорость и характеристическое сопротивление среды равны:

2. Для идеального диэлектрика μ_а=μ₀, ε≠1, σ=0 и δ=0 и по тем же формулам находим; α=0,

v=1/ =1/ =c/ =3∙10⁸/ [м/с],

а соответствующая длина волны

Λ=v/f=c/f = λ/ . (9)

_в=Z_в= = =120π/ [Ом].

3. Для несовершенного диэлектрика μ_а=μ₀, удельная проводимость незначительная (σ«ωε_а) и в соответствии с (4) плотность тока проводимости значительно меньше плотности тока смещения (j_{пр m}«j_{cм m}), угол потерь δ=arctg(σ/ωε_а) мал — порядка 10^-3 ... 10^-4. Тогда

и по формулам (5), (7), (8) находим

α=ω δ/2,

v=1/ =1/ =c/ =3∙10⁸/ [м/с],

Z_в= = = =120π/ [Ом].

4. Для неидеального проводника удельная проводимость настолько большая, что σ»ωε_а и j_{пр m}»j_{см m} в связи с чем комплексная диэлектрическая проницаемость становится мнимой величиной

_а=ε_а–jσ/ω≈–jσ/ω,

δ=arctg(σ/ω ε_а) ≈ π/2.

Если к тому же учесть, что одно из значений =(1+j)/ (в этом можно убедиться при возведении в квадрат обеих частей равенства), то постоянная распространения волны

Вместе с тем =α+jβ. Следовательно, коэффициенты затухания и фазы равны между собой

(10)

а фазовая скорость и характеристическое сопротивление среды

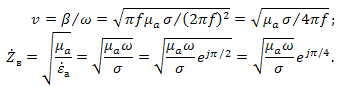(11)

5. Для идеального проводника σ→∞, и в соответствии с формулами (5), (7), (8), получим

α→∞; v=0; Z_в=0. (12)

Выводы:

1. Переход от вакуума к идеальному диэлектрику сопровождается уменьшением фазовой скорости (длины волны) и характеристического сопротивления раз.

2. Несовершенство диэлектрика (σ≠0) практически не влияет на фазовую скорость и характеристическое сопротивление, но на больших дальностях r может вызвать значительное затухание волн α прямо пропорционально углу потерь δ.

3. В неидеальных проводниках очень сильно сказывается увеличение затухания α, уменьшение фазовой скорости v (длины волны Λ) и характеристического сопротивления Z_в, вызванные высокой удельной проводимостью среды. Приведем для сравнения величины α, Λ и Z_в при распространении волн частотой 1 МГц в вакууме и в меди (σ= 5,65-10⁷ См/м):

в вакууме v=3∙10⁸ м/с, Λ=λ=300 м, Z_в=120π= 377 Ом;

в меди v≈421 м/с, Λ≈ 4,21∙10^-4 м, |Z_в| =3,74∙10^-4 Ом.

4. Характеристическое сопротивление вакуума и идеального диэлектрика чисто активное: в этих средах напряженности электрического и магнитного полей совпадают по фазе: _в= =Z_B. В проводящей среде имеется ток проводимости, отстающий на π/2 от тока смещения, и при сложении этих токов вектор H_у не только увеличивается по модулю, но и сдвигается относительно вектора Е_z на половину угла потерь (δ/2). С увеличением σ до ∞ и соответственно δ до π/2 характеристическое сопротивление среды уменьшается до нуля и фазовый сдвиг между _z и _y достигает 45.

5. Свойства полупроводящей среды зависят от частоты f. Это явление называется дисперсией, а сама среда диспергириющей. Примерами диспергирующих сред являются морская вода — довольно хороший проводник при f<9 МГц и диэлектрик при f>9∙10⁴ МГц, сырая почва — проводник при f<18 кГц и диэлектрик при f>180 МГц.

Заметим также, что глубина проникновения электромагнитных волн в проводник (неидеальный) приблизительно равна длине волны Λ. Поэтому в устройствах СВЧ достаточно покрыть поверхность даже плохого проводника слоем серебра толщиной в несколько микрон, чтобы резко снизились его сопротивление и потери, связанные с ним; в идеальный же проводник, для которого v=0 и Λ=v/f=0, электромагнитные волны совсем не проникают.

Р

(13)

асстояние прямой видимости при отсутствии атмосферной рефракции (геометрический горизонт)

км,

где h₁, h₂ – высоты передающей и приемной антенны в метрах.

Р

(14)

асстояние прямой видимости при нормальной атмосферной рефракции (радиогоризонт)

км.

Критическая частота

(15)

,

где N – электронная концентрация слоя ионосферы (N – в э/см³, f – в кГц).

2 Ход работы

2.1. Определить мощность излучения в свободном пространстве на расстоянии r от направленного излучателя с коэффициентом направленного действия D, если амплитуда напряженности электрического поля _m ,а частота f. На какой угол при этом отстаёт фаза поля излучения. Исходные данные приведены в таблице 1.

Таблица1

N вар	6
r, км	9
D	60
m В/м	60
f МГц	350