Пример работы машины Тьюринга

Допустим, на ленте есть слово, состоящее из символов #, $, 1 и 0. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над первой буквой слова слева. Завершается программа тогда, когда головка оказывается над пустым символом после самой правой буквы слова.

Примечание: длина слова и последовательность символов значения не имеют. На рисунке приводится пример последовательности выполнения команд для конкретного случая. Если на ленте будет другое слово, то и последовательность выполнения команд будет другой. Несмотря на это, данная программа для машины Тьюринга применима к любым словам описанного внешнего алфавита (соблюдается свойство применимости алгоритма ко всем однотипным задачам – массовость).

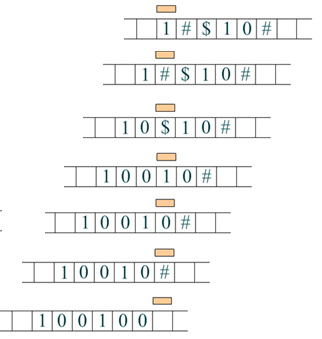
Можно усложнить программу. Допустим, головка располагается не обязательно над первым, а над любым символом слова. Тогда программа для данной машины Тьюринга может быть такой (а могла бы быть и другой):

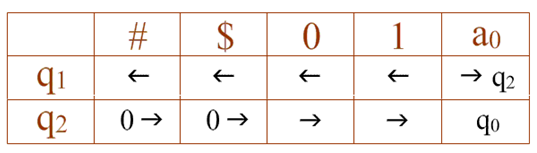
Задача. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над любой буквой слова.

Даны два целых положительных числа в десятичной системе счисления. Сконструировать машину Тьюринга, которая будет находить разность этих чисел, если известно, что первое число больше второго, а между ними стоит знак минус. Каретка находится над левой крайней цифрой левого числа.

1.3 Практическое применение результатов теории алгоритмов

Полученные в теории алгоритмов теоретические результаты находят достаточно широкое практическое применение, при этом можно выделить следующие два аспекта:

Теоретический аспект: при исследовании некоторой задачи результаты теории алгоритмов позволяют ответить на вопрос: является ли эта задача в принципе алгоритмически разрешимой. Для алгоритмически неразрешимых задач: возможно ли их сведение к задаче останова машины Тьюринга. В случае алгоритмической разрешимости задачи возникает следующий важный теоретический вопрос: о принадлежности этой задачи к классу NP–полных задач*. При утвердительном ответе на вопрос о принадлежности к классу NP–полных задач можно говорить о существенных временных затратах для получения точного решения для больших размерностей исходных данных.

*

Алфавитом называется всякое конечное множество символов (например, {0, 1} или {a, b, c}). Множество всех возможных слов (конечных строк, составленных из символов этого алфавита) над некоторым алфавитом  обозначается ^*. Языком L над алфавитом  называется всякое подмножество множества ^*, то есть L^*.

Задачей распознавания для языка L называется определение того, принадлежит ли данное слово языку L.

Язык L₁ называется сводимым (по Карпу) к языку L₂, если существует функция f: ^*^* ,, вычислимая за полиномиальное время, обладающая следующим свойством: f(x) L₂ тогда и только тогда, когда x L_1 .

Язык L₂ называется NP-трудным, если любой язык из класса NP сводится к нему. Язык называют NP-полным, если он NP-труден, и при этом сам лежит в классе NP.

Таким образом, если будет найден алгоритм, решающий некоторую (любую) NP-полную задачу за полиномиальное время, то все NP-задачи окажутся в классе P, то есть будут решаться за полиномиальное время.

Примеры:

• Задача о выполнимости булевых формул

• Кратчайшее решение «пятнашек» размера n×n

• Задача коммивояжёра

• Сапер (игра)

Практический аспект: методы и методики теории алгоритмов позволяют осуществить:

• рациональный выбор из известного множества алгоритмов решения данной задачи с учетом особенностей их применения (например, при ограничениях на размерность исходных данных или объема дополнительной памяти);

• получение временных оценок решения сложных задач;

• получение достоверных оценок невозможности решения некоторой задачи за определенное время, что важно для криптографических методов;

• разработку и совершенствование эффективных алгоритмов решения задач в области обработки информации на основе практического анализа.