14. Закон розподілу Пуассона.

Пуассонівський закон розподілу – це закон розподілу випадкової величини, заданий таблицею, у якій ймовірність обчислюється за формулою Пуассона  .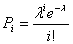

14. Закони розподілу неперервних величин.

14. Нормальний закон розподілу.

Нормальний розподіл або розподіл Гауса є найбільш універсальним, зручним і широко застосовуваним.  Вважається, що напрацювання підпорядкована нормальному розподілу (нормально розподілена), якщо щільність розподілу відмов (ПРО) описується виразом: 

де a і b - параметри розподілу, які за результатами випробувань приймаються: 

де   _0,   - Оцінки середнього напрацювання та дисперсії.

14. Статистична гіпотеза. Основні поняття і принципи перевірки.

Гіпотеза - це наукове припущення, яке потребує перевірки, доведення. Під статистичною гіпотезою слід розуміти припущення про властивості випадкової величини, яке може бути перевірене за результатами статистичних спостережень. Статистичні гіпотези відносяться або до виду, або до окремих параметрів розподілу випадкової величини.

Висунуту гіпотезу, яку потрібно перевірити, називають нульовою. Гіпотезу протилежну нульовій, називають альтернативною.

Перевіряють нульову гіпотезу відносно альтернативної за даними вибіркового спостереження. Суть перевірки статистичної гіпотези зводиться до вибору 3 можливих двох взаємовиключаючих (альтернативних) рішень одного вірного. Наприклад, при вивченні впливу стажу роботи робітників на їхню продуктивність праці можлива альтернатива: а) збільшення стажу роботи робітників сприяє росту продуктивності праці; б) збільшення стажу роботи робітників не сприяє їх продуктивності праці.

Так як нульовій гіпотезі завжди протистоїть альтернативна гіпотеза, яка заперечує її, однак, при формальному підході, будь-яку з цих гіпотез можна розглядати як нульову. Тому вибір однієї з конкуруючих гіпотез як нульової потребує статистичного обґрунтування.

Принципи обґрунтування та прийнятгя рішень в умовах випадкової варіації досліджуваних чшшиків розроблені вченими статистиками і математиками: К. Пірсоном, Е. Нейманом, А.Н. Колмогоровим, Б.С. Ястремським, В.І. Романовським, Р.Фішером та ін.

Аргументація економічного обґрунтування при формуванні нульової гіпотези повинна враховувати також можливі помилки при перевірці статистичних гіпотез.

14. Принципи формування раціональних підгруп даних.

14. Встановлення наявності зв'язку між ознаками. Коефіцієнт кореляції.

Кореляційний зв’язок проявляється в середньому, для масових спостережень, коли кожному значенню ознаки х відповідає певна множина ознаки у, які варіюють і утворюють ряд розподілу. Прикладом такого зв’язку можна навести залежність між рівнем кваліфікації та продуктивністю праці або залежність між кольором очей та кольором волосся.

Коефіцієнт кореляції – показник, який використовують для вимірювання щільності зв'язку між результативними і факторними ознаками у кореляційно-регресійній моделі за лінійної залежності. За абсолютною величиною коефіцієнту кореляції коливається в межах від -1 до +1. Чим ближчий цей показник до 0, тим менший зв'язок, чим ближчий він до ±1 – тим зв'язок тісніший. Знак «плюс» при коефіцієнті кореляції означає прямий зв'язок між ознаками х і у, знак «мінус» – обернений.

Уперше коефіцієнт кореляції як показник щільності зв'язку використав К. Пірсон. Спочатку досліджувалася прямолінійна залежність, пов'язана із законом нормального розподілу (А. Браве, К. Пірсон, В. Шеппард та ін.), відтак виникла потреба в дослідженні й нелінійних залежностей. Для вимірювання щільності зв'язку нелінійних залежностей Пірсон запропонував кореляційне відношення із розробкою методів аналізу взаємозв'язку двох змінних було запропоновано теорію часткових і чистих коефіцієнтів кореляції, а також теорію множинної (багатофакторної) кореляції.

Коефіцієнт кореляції між досліджуваними ознаками повинен мати високий рівень достовірності (надійності). Для оцінки достовірності коефіцієнту кореляції обчислюють відношення коефіцієнта до його середньої помилки. Якщо воно дорівнює або більше 3, коефіцієнт кореляції вважають достовірним, тобто зв'язок між досліджуваними ознаками доведений. Якщо відношення менше 3, то не можна зробити висновку про достовірність зв'язку між досліджуваними ознаками. Для більшої надійності досліджень спід брати величину відношення коефіцієнту кореляції до його середньої помилки не 3, а 4. Якщо відношення коефіцієнту кореляції до його середньої помилки більше 3, а число спостережень більше 50, то вважають, що розрахований лінійний коефіцієнту кореляції відображає істотний тісний зв'язок.