4.2. Определение индуктивности внешнего контура гин

Индуктивность прямолинейных участков проводов рассчитывается по формуле:

L_внеш=0.85 ,

L_внеш=0.85 =11.22 Гн.

Выполнив необходимые расчеты, можно определить полную индуктивность разрядного контура ГИН:

L_ГИН=L_{ГИН(соб.)} +L_вн.к+L_н.=13.161 +11.22 +5 =29.38 Гн.

5. Расчет переходных процессов в разрядной цепи гин

На рис.1 приведен контур цепи разряда ГИН.

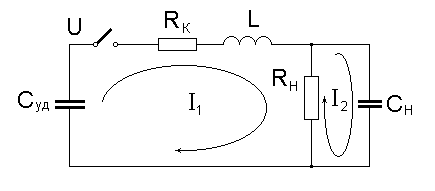
Рис. 1.

Напряжение на нагрузке: где .

Для перехода к оригиналу необходимо произвести преобразования для приведения изображения к табличному виду, имеющему оригинал:

Рассчитаем коэффициенты операторного уравнения - (1), при R_к=0.

a= = ,

b= =

c= .

Для дальнейшего расчета применим формулу Кардано. В уравнении введем новую переменную: . После подстановки уравнение примет вид:

, где: ; ,

q= ,

k= .

Уравнение (1) имеет один действительный корень и два сопряженных комплексных корня. Действительный корень:

где ; ,

u= ,

v= ,

y₁= .

Комплексные корни: ,

y₂= , y₃= .

Далее уравнение необходимо разложить на множители:

,

где , ;

, .

Делая обратную подстановку в последнее уравнение , получим уравнение вида:

где

, .

Расчет напряжения U.

Коэффициент, на который будет увеличено U:

, следовательно U=U_но1.132= кВ.

Определим , .

Рассчитаем форму импульса по формуле:

U(t)= - (1),

,

U1(t)= - (2),

U1(t) = .

6. Уточнение формы импульса гин

6.1. Определение уровня пульсаций и величины добавочного сопротивления

Для того, чтобы уровень пульсаций не превышал заданный: , при построении графика напряжения на нагрузке методом подбора определяем дополнительное сопротивление R_к .

На первом этапе расчета R_к=0, но так как уровень пульсаций превышает заданный, то значение R_к выбираем из диапазона Z_к(кр)> R_к>0, где ,

=138.045Ом.

Методом подбора определяем значение R_к=75 Ом.

Увеличение начального значения R_к ведет к снижению напряжения на нагрузке U_н, поэтому, возникает необходимость увеличения коэффициента до величины 1.256. Тогда, напряжение составит U=1.256U_но= кВ.

Также добавочное сопротивление влияет на емкость ГИН в ударе:

C_уд Ф,

и количество ступеней ГИН: n=23.

Таким образом, сопротивление R_к будет распределяться по ступеням ГИН равномерно:

Ом.

От значения U зависит выбор напряжения источника заряда ГИН, которое должно иметь на выходе напряжение не менее U_зар= U/n = 442.9 /23 = 19.26 кВ.

С учетом U=442.9 кВ и R_к=75 Ом форма импульса будет определяться по формуле:

U1(t) = .

При t=0 U1=350 кВ, при t=180 U1=188 кВ, U_max=378.9 кВ, ΔU=28.89 кВ.

Определим уровень пульсаций по формуле ,

6.2. Определение фронта и длины волны

На рисунках 1 и 2 представлены графики напряжения на нагрузке.

По графику, представленном на рисунке 1, находим длительность спрямленного фронта волны , с.

Определим погрешность %,

.

По графику, представленном на рисунке 2, находим длину волны , с.

Определим погрешность %,

.

Погрешности и не превышают допускаемые ГОСТом отклонения:

_ф= 13%, _и = .