2.1 Дискретизация непрерывных сигналов по в.А.Котельникову
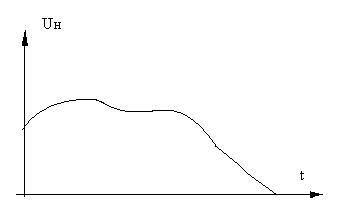
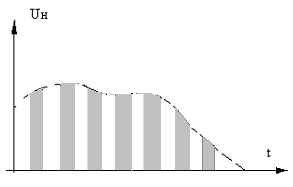
В 30-х годах ХХ столетия значительно вырос интерес к теории и практике дискретизации непрерывных сигналов, т.е. представлению их последовательностью прямоугольных импульсов. Это было вызвано тем, что с помощью данной дискретизации удается получить двойной выигрыш: обратить более уязвимый помехами непрерывный сигнал в менее уязвимый – дискретный и осуществить временное уплотнение каналов связи (т.е. передавать сообщения от нескольких источников по одной линии связи, что дает высокий экономических эффект в силу значительной стоимости проводных линий связи). Временное уплотнение иллюстрируется рисунком.
б)
в)
в`)
г)
Рисунок 1.2 - Система передачи непрерывных сигналов с дискретизацией: а)- временные диаграммы в узлах идеальной (без помех) системы данного типа: б)- в т.т.2,11; в)- внутри дискретизатора после дискретизации по времени; в`)- в т.т. 3,10; г)- В т.т. 4,9.
ИС1 ОС1 ВФ1
Источник непрерывных сообщений |
|
Огрни читель спектра |
|
Восстанавливаю щий фильтр |
ИС2 ОС2 
ВФ2
Источник непрерыв ных сообщений |
|
Ограни читель спектра |
|
Тракт элекро связи |
|
Восстана вливаю щий фильтр |
.
.
. .
. ИСn ОС2 ВФn .
Источник непрерыв ных сообщений |
|
Ограни читель спектра |
|
Восстана вливаю щий фильтр |
Рисунок 1.3 - N – канальная система связи с источниками непрерывных сообщений и
временным уплотнением.
Ω
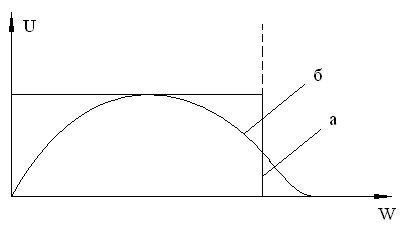
Рисунок 1.4 Амплитудно-частотные характеристики идеального ФНЧ (а) и
реального (б)
Исследовав возможность дискретизации и обосновывая ее теорию, В.А.Котельников доказывал свою знаменитую теорему, лежащую в основе дискретизации непрерывных сигналов. Она гласит: «Непрерывный сигнал, представляемый функцией времени и не имеющий частотных составляющих выше некоторой частоты fв, вполне определяется своими отсчетами (отсчеты Котельникова), взятыми через интервал времени Δt, равный
Δt=1/2fв, (1.1)
где fв – верхняя частота спектра сигнала
Данная теорема обосновывает возможность передачи непрерывного сигнала по дискретному каналу и восстановление его формы на приеме и обеспечивает временное уплотнение трактов электросвязи.
Ограничение, накладываемое автором теоремы на дискретизируемый непрерывный сигнал (отсутствие гармонических составляющих выше fв), отнюдь не устраняет ее практическое применение. Дело в том, что все реальные сигналы имеют конечный спектр (т.е. конечную fв); более того, в подавляющем большинстве случаев спектр реальных сигналов еще сужается за счет ограниченной полосы частот, отводимой им в системах связи. Так, в телефонных каналах речевому сигналу, имеющему спектр 12-15 кГц, отводится полоса частот в 3 кГц; в радиовещании на один канал отводится 10 кГц, в то время как музыкальные передачи требуют для неискаженного воспроизведения полосу пропускания в два раза более широкую.
Итогом дискретизации по В.А.Котельникову является представление заданного непрерывного сигнала Uн(t) рядом, являющимся суммой ортогональных функций вида
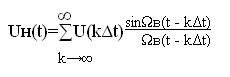(1.2)
где k – число членов ряда, U(kΔt) – амплитуда к-й ортогональной функции (равна амплитуде к-го импульса – отсчета В.А. Котельникова); Ωв – верхняя круговая (циклическая) частота спектра сигнала: Ωв=2πfв; Δt – шаг дискретизации по времени, определяется теоремой В.А. Котельникова (1.1).
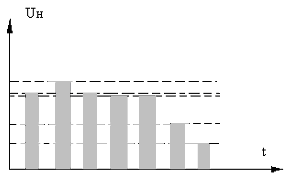
Итак, при рассматриваемой дискретизации непрерывный сигнал Uн(t) заменяется на входе премного тракта последовательностью пряоугольных импуьсов, взятых через промежутки Δt. Эта последовательность может быть обращена в дискретный сигнал (если тот стоит как задача); в этом случае в дискретизаторе осуществляется, вслед за дискретизацией по времени, вторая операция – квантование по уровню (это имеет место в рис. 1.2), когда амплитуда импульса округляется до ближайшего уровня.
Однако, когда при дискретизации по В.А. Котельникову ставится задача
Только временного уплотнения каналов, а не обращения непрерывного сигнала в дискретный, квантование по уровню отсутствует. Тогда все импульсы по амплитуде равны мгновенным значениям Uн(t) в точках отсчета (Δt,2Δt,...,kΔt), и эти импульсы сразу подаются на модулятор (чаще всего здесь используется амплитудная модуляция).
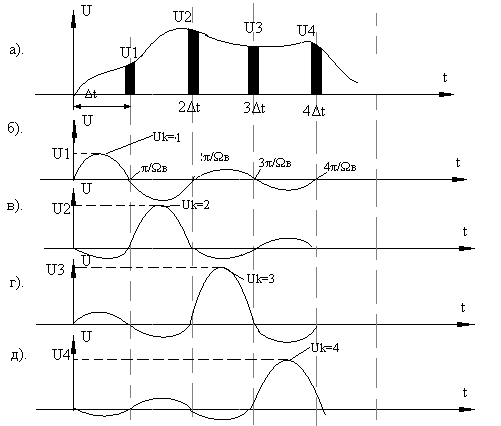
Рисунок 1.4
Что же представляет собой «k» функций под знаком суммы в (1.2)? Оказывается (это легко проверить построением), функции Uk sinxk/xk(а мы наблюдаем под знаком суммы именно «k» таких функций, меняются только Uk и xk) – имеют вид представляемый на рис. 1.5. Но, что замечательно, реакция фильтра нижних частот (ФНЧ) с верхней частотой fв (чтобы не пропускать частоты, большие чем fв – ведь этих частот в спектре дискретизируемого сигнала не должно быть) – Указанная реакция на единичный прямоугольный импульс с амплитудой Uк имеет точно такой же вид – при идеальном ФНЧ (амплитудно-частотную характеристику – АЧХ – такого фильтра (рисунок 4а).
Следовательно, если подать на идеальный ФНЧ (с верхней частотой fв) последовательность прямоугольных импульсов, полученную при дискретизации непрерывного сигнала Uн(t) по В.А. Котельникову, то сумма реакций данного фильтра на все импульсы дает U(t), весьма приближающуюся к Uн(t).